Оставить спектр 5-го порядка. ФЛФ. З-ча 30-4.

[Uchitel'_istorii]

Условие английское:

PNG. писал(а):

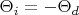
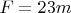
30-4. The spectrograph at the 150 ft solar tower telescope of the Mt. Wilson Observatory is of the Littrow type, shown schematically in the figure. In this instrument, a single lens acts as both the collimator and camera lens, and $\Theta _i = -\Theta _d$ (nearly). The spectrum is formed in a strip adjacent to the slit. The focal length of the Mt. 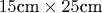Wilson instrument is $F = 23 m$ , and the grating has a ruled area $15 \text{cm}\times 25 \text{cm}$ with $600\text{lines mm}^{-1}$. 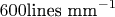The fifth order spectrum is commonly used.

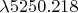
a) At what angle $\Theta$ should the grating be tilted to bring the line $\lambda 5250.218$ of neutral iron in coincidence with the entrance slit in the fifth order spectrum?
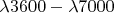
b) What other wavelengths in the range $\lambda3600 - \lambda 7000$ will also be coincident with the slit?
c) Suggest a simple way to remove the unwanted orders, leaving only the fifth order.
d) What is the dispersion of the instrument at fifth order $\lambda 5250$?
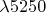
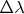
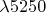
e) What is the minimum $\Delta\lambda$ which can theoretically be resolved at fifth order $\lambda 5250$ by this insrument?

Условие русское:

PNG писал(а):

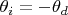
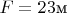
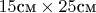
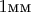
30.4. Спектрограф 150-футового солнечного башенного телескопа, находящегося в обсерватории Маунт Вильсон, показан схематически на рисунке. В этом устройстве одна и та же линза действует и как коллиматорная, и как камерная, $\theta_i = -\theta_d$(почти!). 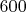Фокусное расстояние всего устройства $F = 23 \text{м}$ а решетка имеет площадь $15 \text{см} \times 25 \text{см}$, причем в $1 \text{мм}$ ее содержится $600$ линий. Обычно при наблюдениях используется спектр пятого порядка.

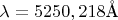
а) При каком угле $\theta$ наклона решетки линия спектра возбуждения нейтрального атома железа, отвечающая длине волны $\lambda=5250,218 \mathring{\text{A}}$, будет совпадать с положением щели в спектре пятого порядка?

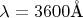
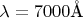
б) Для каких других длин волн в интервале от $\lambda=3600 \mathring{\text{A}}$ до $\lambda=7000 \mathring{\text{A}}$ линия спектра также будет совпадать с положением щели?

в) Предложите простой способ устранения в наблюдаемой картине спектров нежелательных порядков, оставив только спектр пятого порядка.

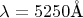
г) Какова дисперсия рассматриваемого устройства при длине волны $\lambda=5250\mathring{\text{A}}$, отвечающей линии в спектре пятого порядка?

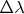
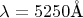
д) Каково минимальное теоретическое значение $\Delta\lambda$, которое может быть разрешено при длине волны $\lambda=5250\mathring{\text{A}}$ в спектре пятого порядка?

Интересует вопрос C). Согласно секции 30-2 лекции 30 , добиться исключения спектров других порядков можно , сделав профиль дифракционной решетки несимметричным пилообразным. И якобы в таком случае получатся пары антенн с разной относительной фазой и разной амплитудой. Однако я не вижу , как разная амплитуда и фаза поможет избавиться от каких-либо спектров.
Допустим, имеем решетку, каждая линия является парой осцилляторов с суммарным полем:
$A_1 e^{i\omega t} + A_2 e^{i\omega t} e^{i\alpha}$
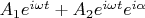
$\alpha$ -- относительная разность фаз в каждой паре.
Для следующей линии:
$A_1 e^{i\omega t}e^{i\phi} + A_2 e^{i\omega t} e^{i\alpha} e^{i\phi}$
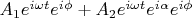
$\phi$ -- относительная разность фаз между соседними линиями.

Просуммировав по всем линиям, получим результирующее поле:
$A = (A_1 + A_2 e^{i\alpha})e^{i\omega t} \sum\limits_{n=0}^{N-1}e^{in\phi}$
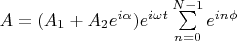
$N$ -- количество линий решетки.

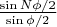
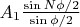
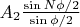
Из лекции 30 известно, что последний множитель дает вклад в амплитуду $\frac{\sin N\phi/2}{\sin \phi/2}$. Т.е. получаем 2 вектора с модулями $A_1 \frac{\sin N\phi/2}{\sin \phi/2}$ , $A_2\frac{\sin N\phi/2}{\sin \phi/2}$ и с углом между ними $\alpha$. Тогда результирующая амплитуда поля решетки запишется:
$|A| = \sqrt{{A_1}^2 + {A_2}^2 + 2A_1A_2\cos{\alpha}} \frac{\sin N\phi/2}{\sin \phi/2}$.

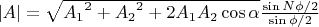
Это мало чем отличается от амплитуды поля решетки с линиями как единичными осцилляторами:
$|A| = A\frac{\sin N\phi/2}{\sin \phi/2}$.

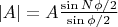
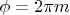
При тех же самых углах , которые соответствуют $\phi = 2\pi m$, где $m$ -- порядок спектра, -- будут наблюдаться максимумы. Интенсивность всех максимумов (а не отдельно взятого) будет зависеть от угла $\alpha$.

В решебник пока не заглядывал, хочу понять, можно ли решить задачу с той информацией, что дана в лекции 30.

[se-sss]

Моя первая мысль по поводу 3-го вопроса - это сделать что-то весьма очевидное, но вообще не связанное с решёткой.
Но не уверен, что авторы задачи думали об этом же.

[Uchitel'_istorii]

Просмотрел ответ (а также ответ задачи 30.6) PNG, и он меня не обрадовал. Более качественный рисунок показывает PNG, что формула решетки должна быть $d\sin(2\varphi) = m\lambda $.

Однако вершины пилообразного профиля рассеивают свет во всех направлениях и создают максимумы всех порядков. Поверхность ступеньки же просто отражает белый свет ($d < \lambda$ , $m=0$). Таким образом получаем все максимумы, один из которых подсвечен белым светом.