Очередная задача про "шары" и "ящики"

[omanovich]

Приветствую всех. Недавно в моей жизни появилась одна задача, для решения которой нужно написать код. Суть этой задачи такова: есть $n$ ящиков и $m$ типов шаров. Нужно раскидать эти шары по всем ящикам таким образом, чтобы а) все ящики были примерно равно заполнены и б) разброс шаров одного типа по всем ящикам был как можно более равномерен.
При этом накладываются ограничения:
1) известно заранее количество шаров каждого типа и их нужно разложить абсолютно все
2) на каждый тип шаров накладывается ограничение по расположению (я дальше объясню).

В математике я не силен абсолютно, но вот, что я сделал:
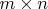
1) для начала представил всю задачу в виде матрицы $m \times n$, где в узлах элемент $a_{ij}$ соответствует количеству шаров типа $i$ в ящику $j$. По условиям задачи на эту величину накладываются условия, что в некоторые ящики шары одного типа класть нельзя ($a_{ij}=0$), или их не должно быть меньше определенного количества ($a_{ij} \geq k_{ij}$). Причем значение $k_{ij}$ мы знаем, но оно может быть любым. Сделал это для удобства представление, но, как я понял это просто вектор размерности $mn$.
2) составил целевую функцию, где через метод наименьших квадратов записал условия а и б. Размер шаров и их "ценность" не имеют значения т.к. они все одного размера и одной ценности. Эту функцию нужно минимизировать при условиях из предыдущего пункта.

После этого для меня начался ад, потому что пришлось лезть в такие места, о существовании которых я и не подозревал. Соответственно мне нужна помощь с выбором стратегии решения этой задачи. Как я понял это np-полная задача (прав ли я?) и решать ее можно методом ветвей и границ, но я не знаю, как выбрать функцию ветвления и нижнюю границу. Или, как вариант, убрать условие целочисленности и решать обычную непрерывную задачу, а в конце округлить? Природа количества шаров сама по себе не очень точная и в каких-то разумных пределах может меняться, если очень захотеть. Но по этому пути я идти не хочу, хочу разобраться и сделать правильно. Заранее спасибо

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[omanovich]

Решил задачу кривым способом, т.е. сначала получил непрерывное решение а после округлил его. Но до сих пор думаю над целочисленным подходом