Ivan_B, для исправления Ваших рассуждений не нужно доказывать, что сумма периодических функций есть почти периодическая функция. Вот здесь
Цель - доказать, что для любого

существует

, при котором модуль разности равен

:
Пусть такого

не существует, тогда модуль разности всегда больше

. Модуль разности непрерывный, поэтому если зафиксировать

и менять

функция примет свое минимальное значение

(

можно не включать, поскольку

) Это приводит к противоречию, поскольку для

найдется

, такое что для всех

верно

. Если взять

, то

.
достаточно исправить последнюю строку и, исходя из всюду плотности, для данных

выбрать

такой, что

, где

стремится к нулю. Тогда мы можем сколь угодно приблизиться к интересующему нас модулю разности и при достаточно больших

получить противоречие. Замечу также, что ничто Вам не мешает брать

в качестве точки максимума этого модуля разности и получить, что
при всех
![$x_{1} \in [0,T_{1}],x_{2} \in [0,T_{2}]$ $x_{1} \in [0,T_{1}],x_{2} \in [0,T_{2}]$](https://dxdy-04.korotkov.co.uk/f/7/0/b/70b22844ec0adf2cf4a5130aeae385db82.png)
. Отсюда вытекает, что

, что противоречит тому, что периоды были несоизмеримы.
И если уж пользоваться всюду плотностью

, то лучше сразу сказать, что

для некоторой целочисленной последовательности

и

. Тогда

. Но как я уже сказал
выше, в данной конкретной задаче это не нужно и все оказывается проще.
К вопросу про почти периодические функции. Чтобы показать, что сумма двух периодических функций почти периодическая лучше использовать критерий Бохнера:
ограниченная непрерывная функция 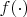 почти периодическая тогда и только тогда когда из любой последовательности ее сдвигов
почти периодическая тогда и только тогда когда из любой последовательности ее сдвигов  ,
,  , можно выделить равномерно сходящуюся подпоследовательность.
, можно выделить равномерно сходящуюся подпоследовательность. Из него почти периодичность суммы/произведения п. п. функций очевидны. Без этого критерия, напрямую, доказательство есть у Безиковича (A. S. Besicovitch. Almost Periodic Functions. 1954), но это долго и муторно. Так что не советую туда заглядывать

. Доказательство критерия Бохнера не такое уж и трудное, если думать в терминах

-сетей и доступно для самостоятельного вывода хорошему студенту-третьекурснику знакомому с критерием предкомпактности Хаусдорфа и подобными трюками. Так что если пока сложно/не доросли, то лучше оставьте это.
Замечу, что утверждение
если функция
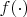
почти периодическая и

при

, то

.
доказывается одинаково просто при любом определении почти периодической функции.



