Попробовал построить

-критерий. Для начала введем еще пару обозначений: гипотезу

обозначим как

, гипотезу

обозначим как

. Строим

-критерий для случая, когда

нулевая,

альтернативная. Зададим уровень значимости, например,

. Тогда
с (в уравнении 8 параграфа 54 Севастьянова) будет равно

(критическое значение для

). Для значения

отношение правдоподобия равно
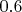
, тогда принимаем нулевую гипотезу, т.е. гипотезу

.
Теперь меняем гипотезы местами, нулевой будет гипотеза

, альтернативной

(имеем право, обе гипотезы простые, оснований для предпочтения нет). Тогда

будет равно

(критическое значение для

). Для значения

отношение правдоподобия равно

, тогда опять принимаем нулевую гипотезу, но теперь это гипотеза

.
Получается решение зависит от того, какая гипотеза нулевая, а какая альтернативная. Обе гипотезы равноправны (Севастьянов упоминает этот случай на стр.196, но я не нашел, где он его рассматривает), назначение нулевой и альтернативной произвольное.
Самое забавное, что если дисперсии обоих распределений равны, то никаких сложностей не возникает.



