Добрый день.
Есть последовательность

. Доказать, что она не имеет предела. Решил построить доказательство через критерий Коши, т.к. слабо с ним знаком.
Для того, чтобы последовательность

вообще имела конечный предел, необходимо и достаточно, чтобы для каждого числа

существовал такой номер
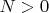
, чтобы неравенство

выполнялось для всех

и

. [Фихтенгольц-1, стр. 83]
Последовательность

не будет иметь конечный предел тогда и только тогда, когда будет существовать некоторое число

такое что, для всех
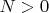
будут существовать

и

такие, что выполнится неравенство

.
На языке логики предикатов определения фундаментальной и нефундаментальной последовательностей имеют вид:
Фундаментальная

Нефундаментальная

Пусть

, а

. Тогда получаем неравенство, из которого необходимо вывести

(проверить, действительно ли такое число существует):

.

--- правильная положительная дробь (за исключением единицы). Поэтому

существует и оно находится в пределах

. Таким образом, какое бы ни взять натуральное
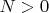
, для него найдется положительное

, находящееся в пределах

, что выполнится неравенство

при

и

.
Собственно вопрос, правильно ли построено доказательство?



