Ссылка на раздел 27-7:
http://www.feynmanlectures.caltech.edu/ ... ml#Ch27-S7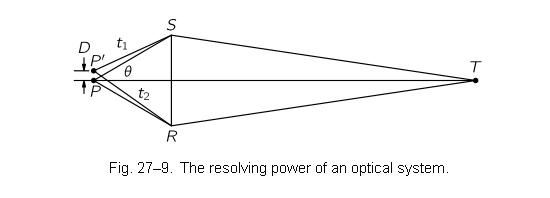
Фейнман пишет, чтобы 2 точки отличить должно выполняться неравенство:


-- частота света.
Или, что полностью идентично :


- угол зрения линзы (opening angle);

- длина волны;

- показатель преломления.
У меня не получается эта формула.
Из рисунка видно , что

меньше соответствующего времени для точки

на величину

,

-- больше на ту же величину. Таким образом разность:


Неравенство принимает вид:


Где ошибка?
Далее , Фейнман пишет, что для телескопа угловой размер между двумя звездами должен быть больше

,

- диаметр линзы телескопа.
Эту формулу также не могу получить.
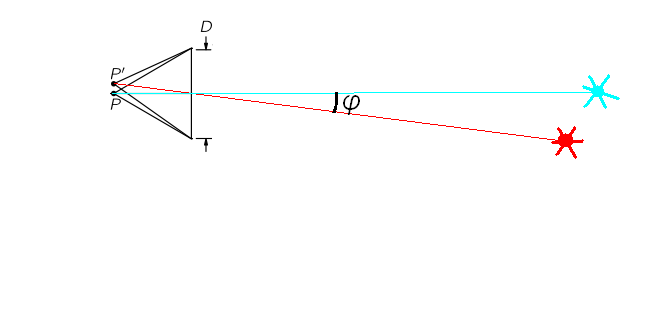
Из рисунка

, где

- фокусное расстояние.

Отсюда формула для телескопа:


Если для

тангенс можно заменить углом, то для

- нет.
Где ошибка?
И в связи с этой темой 3-й вопрос о формуле линзы:

.
Если

, то

. Но

-- это расстояние от объекта на оси до края линзы, а

меряется от центра линзы по оси. Получается, что катет равен гипотенузе. Фейнман упоминал, что сферические линзы работают только для лучей , близких к оси. В этом объяснение ?



