У нас есть некоторое поле

и структура векторного пространства над ним --

. При этом мы можем построить очевидное "воплощение" нашего векторного пространства

в виде

-- арифметического пространства, если, конечно, наше пространство

конечномерно и имеет размерность

.
Рассмотрим множество всех линейных отображений из нашего в.п.

в некоторое другое пространство

, строго над тем же полем

и обозначим его, например, как

. Это множество можно наделить структурой векторного пространства с групповой операцией вида

и

, где

. Тут же напрашивается изоморфизм арифметического пространства

с пространством функций из
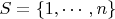
, где

в поле

, что очевидно представляется в виде

. Базисом будут характеристические функции

, принимающие значение

только на тех элементах множества

, которые совпадают с ординалом

и значение 0 на всех остальных элементах

.
Пространство многочленов
![$K[x]_{\leq}$ $K[x]_{\leq}$](https://dxdy-04.korotkov.co.uk/f/3/7/2/37213b54046a71f3e0f9850ccbb9c29982.png)
степени не выше

изоморфно

-мерному координатному пространству

, посредством биективного отображения, сопоставляющего каждому многочлену набор его коэффициентов в

. А вместе с ним получаем и изоморфизм
![$K[x]_{\leq}$ $K[x]_{\leq}$](https://dxdy-04.korotkov.co.uk/f/3/7/2/37213b54046a71f3e0f9850ccbb9c29982.png)
и

.
Если в


, то мы получаем множество всех линейных преобразований пространства

. На этих преобразованиях явно сохраняется групповая структура из

. При фиксации базиса можно построить изоморфизм. Первый вопрос:

-- это

? В

разве та же самая групповая операция?
Тут же возникает конструкция двойственного линейного пространства

, которая строится на тех

, в которых

, а

-- одномерное векторное пространство поля над самим собой. При этом в

существуют такие отображения, которые устанавливают изоморфизмы вида, например,

или неканонический изоморфизм

. В двойственном пространстве можно рассмотреть подпространства, образованные билинейными формами, а также подпространство квадратичных форм. По билинейным формам строится канонический изоморфизм пространства и его двойственного пространства. При этом элементы этих подпространств представимы в виде многочленов из
![$K[x]_{\leq}$ $K[x]_{\leq}$](https://dxdy-04.korotkov.co.uk/f/3/7/2/37213b54046a71f3e0f9850ccbb9c29982.png)
.
Теперь рассмотрим кольцо матриц

. Группа обратимых матриц порядка

называется

, c операцией матричного умножения. При этом она явно изоморфна группе

. А всё кольцо матриц

изоморфно

. Но здесь существует нюанс: такой изоморфизм всегда явно зависит от выбранного в пространстве

базиса. Второй вопрос: какая вторая "кольцевая" операция в

?
В

можно выделить подгруппу

. В

есть подгруппы
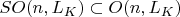
.

.
Я привожу все утверждения без доказательств, потому что хочу наметить в голове некоторый "скелет" линала. Подскажите, насколько мне удалось его верно выделить? И можно ли это красиво записать в виде диаграмм? Может быть уже есть такие схемы? А то, пока переберешь все эти конструкции в голове, уже успеешь порядочно запутаться...



