Во-первых, заметим, что

дает решение. В дальнейшем будем предполагать, что

.
Перепишем уравнение в виде

и заметим, что НОД

делит

.
Так как

делит

, что в свою очередь делит

, то

.
Поэтому исходное уравнение распадается на два:

,
где

- нечетные,

,

и

.
Выражая

двумя способами, получаем:

Заметим, что равенство
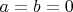
невозможно, так как левая часть в этом случае четна (в виду того, что

), а правая - нет. Поэтому

.
Если

, то с необходимостью имеем

, что дает уравнение:

которое не имеет нечетных целочисленных решений (в виду того, что при ненулевых

имеет место неравенство

)
Предположим, что

, и рассмотрим следующие случаи:
i) Случай

невозможен из-за соображений четности.
ii) Если

то с необходимостью имеем

, что невозможно.
iii) Если

то с необходимостью имеем

и

, что дает уравнение:

или

которое опять же не имеет нечетных целочисленных решений (см. выше).
iv) Если

то

, что невозможно.
Вывод:

- единственные решения исходного уравнения.



