Проверка гипотезы

[Insearch]

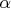
В выборке объема $n содержиться $m бракованных элементов. Проверить гипотезу о том, что на уровне значимости $\alpha в генеральной совокупности количество бракованных элементов не менее $a_0%.

Ни сама выборка, ни закон распределения не заданы.

На сколько я понимаю нулевая гипотеза будет состоять в равенстве выборочного мат. ожидания заданному: $H_0: M_n(X)=a_0, $M_n(X)=(m/n)*100%.

Тогда $H_1: M_n(X) \ge a_0.

Далее необходимо определиться с наблюдаемым значением и из соотношения $P(Z_a_c_t<Z_t_h_r)=\alpha определить пороговое значение $Z_t_h_r и при попадании наблюдаемой величины в интервал $Z_a_c_t \ge Z_t_h_r - принимать гипотезу.

Вопрос первый. Верен ли выбранный нулевой критерий?

Вопрос второй. Что из себя представляет наблюдаемое значение и какое оно имеет распределение?

У Гмурмана описано несколько вариантов формирования наблюдаемого значения, но для проверки гипотез относительно равенства мат. ожиданий необходимо либо знание дисперсии, либо получить её исправленную оценку, ни того, ни другого по условию задачи нет.

Как всегда, благодарен за ответы!

[faruk]

Insearch писал(а):

Ни сама выборка, ни закон распределения не заданы.

Из N элементов генеральной совокупности, содержащей M бракованных элементов, проверяются n элементов, среди которых обнаруживаются m бракованных элементов. -- Гипергеометрическое распределение.
Но поскольку M неизвестно, а, наоборот, должно быть оценено статистически, то в случае $N>>n$ гипергеометрическое распределение можно заменить биномиальным, которое в свою очередь может быть заменено нормальным, если выполнены соответствующие требования.

[Insearch]

Цитата:

гипергеометрическое распределение можно заменить биномиальным, которое в свою очередь может быть заменено нормальным, если выполнены соответствующие требования

Ну хорошо, функция распределение известна, но вопрос с наблюдаемым значением остается открытым.

Допустим, я напишу формулу для оценки вероятности в случае гипергеометрического распределения: $P(m)=C_M^mC_N^n_-^-_M^m/C_N^n. Как можно связать эту вероятность с уровнем значимости?

Прошу помощи, т.к. не вижу направления движения.

[antbez]

Это- неверная формула

[Insearch]

antbez писал(а):

Это- неверная формула

Поправил. Как быть с уровнем значимости?

[antbez]

А как Вы проверяете гипотезу? Возьмите, к примеру, критерий Пирсона. Там и уровень значимости обретёт смысл...

[faruk]

Insearch писал(а):

Прошу помощи, т.к. не вижу направления движения.

Для лучшего понимания сути проблемы попробуйте сначала решить обратные задачи:
Имеется неограниченное количество элементов с долей бракованных $a_0$.
1) С какой вероятностью в выборке объемом в n элементов содержится не менее m бракованных?
2) При каком значении $p=\frac{m}{n}, p>a_0$ вероятность такой выборки не более $\alpha$ ?

[GAA]

Я ранее не читал книги Гмурмана В.Е. Cкачав книгу «Теория вероятностей и математическая статистика» (2003) и бегло просмотрев оглавление, нашел в главе 12 §18 «Сравнение наблюдаемой гипотетической частоты с гипотетической вероятностью». Если Вам, Insearch, рекомендована именно эта книга, посмотрите этот параграф.

Insearch писал(а):

Вопрос первый. Верен ли выбранный нулевой критерий?
(Видимо, автор хотел написать не «нулевой критерий», а нулевая гипотеза. — прим. GAA)

Думаю, что нет. Обозначим долю бракованных элементов в генеральной совокупности через $p$, т.е. $p=M/N$. Нулевая (основная) гипотеза: $p \ge a_0$, альтернатива: $p < a_0$.

Insearch писал(а):

Вопрос второй. Что из себя представляет наблюдаемое значение и какое оно имеет распределение?

Как указал faruk, число бракованных изделий в выборке имеет гипергеометрическое распределение, которое при $M/N \to p = \text{const}$ стремится к биномиальному при стремлении N к бесконечности. (Это уже обсуждалось на Форуме.) Проверку гипотезы о параметра $p$ биномиального распределения можно посмотреть в разделе 7 «Статистическая проверка гипотез (критерии значимости)» второй части лекций И.Н. Володина.