Ok, я приведу картинку и опишу, как её получить. Сама конечная формула выглядит действительно громоздко, не будем бессмысленно загромождать пространство.
Будем пользоваться пакетом Mathematica для расчёта интегралов по пространству из первого сообщения этой темы.
Итак,

. Положим

и введём

.
Первообразная от интегрирования по

имеет вид:

.
Теперь берём интеграл по

, подставляя туда

. Получаем первообразную

. Тоже получается аналитическая формула (я не буду её приводить, много букафф).
После этого берём интеграл по

:

.
Окончательно получаем магнитное поле

. (Там вылезает очень маленькая артефактная мнимая часть, так что надо строить вещественную часть поля)
Теперь мы можем построить график как функцию расстояния вдоль оси

от квантовой точки,

. Возьмём

Эрстед, переведём в СИ (коэффициен

). Пусть

,

,

,

микрон. (То есть мы все расстояния кроме

фиксируем.)
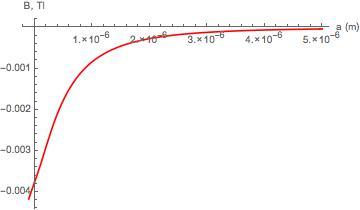
Анализируем - поле резко возрастает по модулю при отходе от точки, а потом быстро убывает.
Теперь можно построить поле под самой точкой. Здесь

- расстояние от одного края точки до другого, остальные параметры такие же. Имеем:
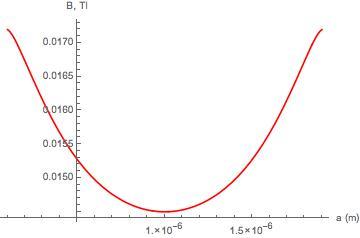
Поле примерно постоянное, подярка 0.015 Tl.



