В прошлой
теме я пытался доказать следующее утверждение.
Утверждение. Пусть

непустое подмножество топологического пространства

(

). Тогда, если

и

- открытые непресекающиеся подмножества множества

(

,
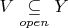
и
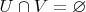
), то существуют такие открытые непересекающиеся подмножества

и

множества

(

,

и

), что
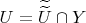
и

.
Контрпример, приведённый в той
теме показал, что моё предположение было неверно.
Однако, в метрическом пространстве это утверждение верно.
Утверждение. Пусть на множестве

задана метрика

и

непустое подмножество множества

(

). Тогда, если

и

- открытые непресекающиеся подмножества множества

(

,
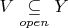
и
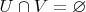
), то существуют такие открытые непересекающиеся подмножества

и

множества

(

,

и

), что
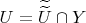
и

.
У меня пока нет идей, как доказать это утверждение, кроме топологических идей, которые я показал в предыдущей
теме.
Подскажите, пожалуйста, какие метрические идеи нужно использовать для доказательства этого утверждения.



