Пусть на множестве

задана топология

.

- непустое подмножество множества

, на которую топология

индуцирует топологию

.
Нужно показать, что если

и

- два непересекающихся открытых подмножеств множества

(

,
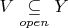
и
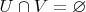
), то существуют два непересекающихся открытых подмножеств множества

(

,

и

) таких, что
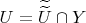
и

.
Вот моя
первая попытка доказательства, которая пока ни к чему не привела.
Так как

и
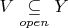
, то
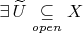
и

такие, что

и

.
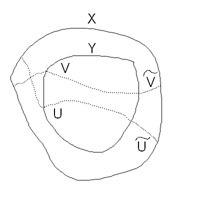
Пусть

и

. Тогда
1)

(легко доказывается),
2)

(очевидно, так как

).
А вот доказать, что
3)

не получается.
Так как, из

следует, что

, то верно включение

. Обратное включение (

) не получается доказать, так как множество
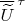
может содержать точки множества

.
Вот если можно было бы в качестве множества

взять такое множество, что

(понятно, что множество
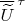
не может пересекать множество

по своему подмножеству

), то утверждение тогда доказывалась. Но, у меня пока не получается такое множество

построить.
Вторая попытка заключается в следующем. Пусть

. Утверждение будет доказано, если я смогу найти такое множество

, что
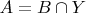
и

. То, что

следует из того, что замыкание множества есть наименьшее по включению замкнутое множество, содержащее само множество. Обратное включение множеств не удаётся пока доказать хотя бы для какого-нибудь

.
Может, есть более простые доказательства моего главного утверждения?