Например, на 67: отнимаете

и делите на 100. С любым другим числом можно поступить точно так же -- избавиться от первой или от последней цифры. Например, на 53:
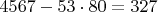
и 53 на 9 больше 327 (последнее вычислять не нужно, только сравнить).
Например, на 53:
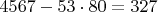
и 53 на 9 больше 327
 На 7 и на 8 - тоже больше
На 7 и на 8 - тоже больше 
А... понял почему на 9.
Ну и скока надо посчитать в уму для сертификации
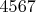
на простоту?
Во-первых, надо извлечь квадратный корень. Он равен упомянутому

, конечно, но его таки надо извлечь.
Затем надо выписать все простые до

включительно, это

и быстренько по 2-3 действия посчитать. По скока секунд, вы думаете, надо потрать на каждое (начиная с

)? Ну еще плюс извлечение корня и выписывание их всех (чтоб никакое не пропустить и не забыть на котором остановился когда зачешется в носу). Думаю минут 10 (а то и больш) как раз и потратится.
Задача какая-то муторная и мне представляется, что
Ktina тут прав(-а): на олимпиадность, кажись, не тянет. В самом деле: как можно НЕ решить эту задачу? Тока если времени не хватит на сертификацию простоты или таблица умножения позбылась.