Попробую тоже дать пояснения. Для ТС. Речь у меня только о случае с
1. Волновая функция частицы с


(где

есть постоянная)
в 3-мерной яме

удовлетворяет уравнению

Это уравнение очевидным образом
отличается от уравнения для волновой функции

частицы в одномерной яме


Очевидным образом различаются и "картины движения" частицы в одномерной и трёхмерной ямах: в одномерной задаче

- вероятность обнаружения частицы в интервале

на линии, а в трёхмерной задаче

- вероятность обнаружения частицы в трёхмерном элементе объёма

с радиус-вектором

направленным под произвольными углами

"Облако вероятности"

- сферически симметричное (поскольку

Оно, в отличие от

не сосредоточено на линии, и поэтому нет смысла объяснять его себе каким-то загадочным "колебательно-поступательным" движением частицы. Различие уравнений для

и

также не даёт повода сопоставлять решения одномерной и трёхмерной задач на основе лишь пальцевых "колебательно-поступательных соображений".
2. Оказывается (так уж повезло с математикой), что подстановкой

уравнение трёхмерной задачи приводится
для вспомогательной функции

к уравнению того же вида, что и для

в одномерной задаче:

(при

Физический смысл у функций

и

разный (функция

не равна плотности вероятности

в трёхмерной задаче), но математический повод сравнивать решения

и

есть, и осталось только разобраться, как сравнивать потенциал

задаваемый на оси

с заданным в трёхмерном пространстве потенциалом

Замечаем, что на вспомогательную функцию

резонно наложить граничное условие

при

чтобы избежать проблем с обращением в бесконечность настоящей волновой функции

при

Чтобы обоснованно наложить такое же условие на

в одномерной яме,

следует выбрать одномерную яму

с бесконечно высокой стенкой при


при

при

Говоря наглядно: в трёхмерной задаче частице недоступны отрицательные значения радиальной координаты
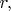
доступны только

поэтому и в соответствующей одномерной задаче мы не разрешаем частице заходить в область отрицательных значений

- ставим при
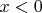
бесконечно высокий потенциальный барьер. Ну, а в области положительных значений аргумента графики одномерного

и трёхмерного

потенциалов пусть себе совпадают; в общем случае при
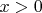
не обязан находиться бесконечно высокий барьер, рельеф ям может быть достаточно произвольным, так что в общем случае речь идёт о какой-то "несимметричной яме".
Понятно, что при таком выборе

решения

и

будут одинаковыми (и уровни

тоже. Нюанс, свойственный несимметричным ямам

: если яма недостаточно "мощная", то в ней нет ни одного уровня. Будем считать, что наши рассматриваемые ямы достаточно мощные).
Смысл квантового числа

в одномерной и трёхмерной задачах разный. В одномерной яме уровни не вырождены, и действует "осцилляционная теорема": волновая функция

нижнего уровня не имеет узлов, а на каждом следующем уровне добавляется один узел. Для нумерации волновых функций и уровней можно воспользоваться этим числом узлов,

С тем же успехом можно воспользоваться определением

тогда нумерацию

и

в одномерной и трёхмерной яме при

можно выбрать одинаковой.
В трёхмерной яме осцилляционная теорема в применении к

позволяет нумеровать функции

числом их узлов

оно одновременно является числом узлов радиальной функции

"Главное квантовое число"

в трёхмерной задаче принято определять формулой

Уровни энергии при произвольном моменте

вырождены по проекции момента

но зависят от
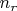
и

Отсюда видно, что при

можно нумеровать уровни и волновые функции "главным квантовым числом"

получается такая же нумерация как и для состояний в одномерной яме

3. Никакой "пропажи" уровней в рассмотренном сюжете нет. "Пропажа" есть в другом сюжете, чисто одномерном. Из рассмотренной выше несимметричной ямы

сделаем симметричную яму

убрав бесконечно высокий барьер при
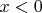
и симметрично доопределив потенциал в область отрицательных


при

при

Все волновые функции, найденные в несимметричной яме, являются решениями и для симметричной ямы, причём, очевидно, они имеют узел в центре ямы (обращаются в ноль при

значит, это нечётные решения:

По осцилляционной теореме волновая функция самого нижнего уровня не должна иметь узлов, и, значит, в симметричной яме должна быть чётной; чётными будут и функции с двумя узлами, с четырьмя и т. д.
Таким образом: нечётные решения для симметричной ямы

являются решениями и для несимметричной ямы

с бесконечной стенкой, расположенной в центре симметричной ямы, а чётные решения пропадают - не являются решениями в несимметричной яме.
В частном случае, когда прямоугольная одномерная яма ограничена бесконечными стенками
с обоих концов, её можно саму по себе рассматривать как симметричную. Но если решения

в ней хочется интерпретировать как

то следует считать эту яму несимметричной: её левая бесконечно высокая стенка находится в точке

соответствующей

Никакой "пропажи" уровней при сопоставлении такой одномерной задачи с трёхмерной задачей нет.



