Ну что ж, если Вам нужна только причина происходящего и совершенно не интересует, как эту проблему решить... давайте займемся причиной.
Я тут слегка приболел и не стал заглядывать в тему. А хотелось бы довести задачу до какого-нибудь решения.
Как Вы думаете, к чему приведет попытка построить решение в сторону

?
Это я понял еще до того, как создал тему, то есть получается тривиальное решение, когда плотность и давление строго нули. Но это значит , что
Dmitriy40 прав и у Иванова и на форуме astronet , такая задача с избыточным краевым условием

ставится не совсем корректно. Поэтому ваши фейспалмы вообще говоря не по адресу.
Я почитал немного про краевые задачи такого типа.
Если фиксировать на

, что для ньютоновских звезд вполне разумно, то решается задача сначала как Коши для условий справа (в конкретном случае), а давление выступает как параметр

. Он вначале выбирается произвольно, а затем методом Стрельбы гоняется таким образом , чтобы удовлетворить условию на другом конце :

.
Тогда надо писать программку. Вроде есть образец.
-- 04.08.2018, 11:23 --Приведу два довода , почему именно для Звезды мне кажется предпочтительнее решать задачу Коши, а не краевую.
Во-первых, скорее всего она имеет сложную структуру и фиксации одного параметра состояния

не обойтись.
Скажем в интервале

одно состояние с
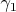
, а в

может быть совсем другое и даже не политропа.
Тогда проще решать именно задачу Коши методом Рунге-Кутта на правом интервале при

, при некотором разумной распределении

, тогда

какая получится. А далее уже решать краевую в интервале

.
А второй довод, когда мы перейдем к поправкам ОТО, то в этом случае

это по смыслу полная масса звезды , включая гравитационное поле, то есть масса, которая входит в решение Шварцшильда. Но это не исключает того, что может быть

.
Об этом пишут Оппенгеймер и Волков , но они эту возможность отбросили, когда зафиксировали политропу. В общем случае такой случай нельзя отбрасывать. Поэтому фиксировать левый край у меня нет оснований. К тому же появились статьи в последние годы по этой теме. Я пока не хочу вступать в дискуссию по данному вопросу. Мне надо поверить одну статью и сконструировать чисто математический объект.