Здравствуйте. Есть задача, с которой долго мучился, поэтому сомневаюсь, что мое решение самое короткое:
показать, что свертка двух эрмитовых (или антиэрмитовых) тензоров есть действительное число.
Т.е. нужно рассмотреть свертку

, где

и
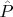
-- эрмитовы или антиэрмитовы тензоры. Пусть для начала они будут эрмитовы, тогда, как я понял, нужно показать что

, ведь именно это является условием вещественности числа.

тупик. Другая попытка:



что без индексов выглядит является разностью следов:

. А теперь c учетом свойства следа, которое заключается в том, что след не меняется при транспонировании, получаем

а это значит, что та разность следов равна нулю и что искомая свертка суть действительное число. Для антиэрмитовых точно так же можно поступить. Можно ли быстрее решить?