Пусть

влечет

. Если

истинно, значит и

истинно. Если

ложно, значит

может быть как истинным так и ложным.
А что, если

неопределенно?
Демидович 135.
Доказать, что если

,

и

, то последовательность

- сходящаяся.
Если

то

начиная c некоторого

Если

, то

Из нижней границы

можно получить верхнюю границу для

Если

, то

Если

- максимальное значение, то
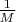
минимальное из

Значит, если

была точной нижней границей

, то
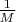
будет точной верхней границей

Если

и

, то

и

Поэтому исходное равенство верно только если

Непонятно как обосновать




