Лагранжиан и "канонические преобразования".

[amon]

Видимо в силу слабой образованности, столкнулся с некой проблемой (для меня, скорее всего, это где-то разжевано). Что бы не лезть в дебри, приведу, как учит Red_Herring, минимальный пример для задания вопроса.
Есть у нас гамильтониан гармонического осциллятора

$$ H=\frac{p^2+q^2}{2} $$

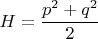
Сделаем "каноническое преобразование" (почему в кавычках - сейчас будет понятно)
\begin{align*} Q&=\frac{q-ip}{\sqrt{2i}}\\ P&=\frac{q+ip}{\sqrt{2i}} \end{align*}
Знатоки квантовой механики узнают здесь переход к операторам рождения (с точностью до множителя $\frac{1}{\sqrt{i}}=e^\frac{-i\pi}{4},$ который нужен для сохранения стандартной скобки Пуассона). Легко проверить, что все скобки Пуассона сохраняются ($\{Q,P\}=1$ и т.д.), а гамильтониан станет $\mathcal{H}=iPQ.$ Поскольку число уравнений удвоилось (кроме $P$ и $Q$ есть еще $P^*$ и $Q^*$), то на систему наложатся еще две связи, означающие, что $p$ и $q$ вещественны:
\begin{align*} Q^*&=iP\\ P^*&=iQ. \end{align*}
Все это хорошо и замечательно, все уравнения дают правильные ответы, и все хорошо, пока мне не придет в голову блажь написать в новых переменных $P$ и $Q$ функцию Лагранжа. Тут выясняется, что влоб это сделать невозможно, так как преобразование Лежандра вырождено, в том числе с учетом связей. Вопрос (видимо в основном к pogulyat_vyshel): что тут не так? Преобразование не каноническое? Есть ли что-то почитать про подобные казусы?

[pogulyat_vyshel]

Я ничего удивительного не вижу. Можно и без комплексных замен тоже самое получить Перейдите в координаты "действие -угол" с помощью канонической замены
$$p=\sqrt{2I}\cos\varphi,\quad q=\sqrt{2I}\sin\varphi$ в новых переменных гамильтониан тоже вырожден $H=I$. Это связано с тем, что в данной системе на всех торах одна и таже частота

[amon]

pogulyat_vyshel в сообщении #1317633 писал(а):

Я ничего удивительного не вижу.

То есть канонические преобразования могут из лагранжевой системы сделать нелагранжеву? Спасибо, я же говорил, что безграмотность и ничего более. Буду думать, как из этого выкрутиться.

[pogulyat_vyshel]

Обычно, в действительном случае (про комплексный не думал) из этого выкручиваются так(пример тотже, $I>0$). Вместо гамильтониана $H=I$ возьмем гамильтониан $\tilde H=I^2$ -- этот уже невырожден. У системы с гамильтонианом $H$ теже траектории в фазовом пространстве, что и у системы с гамильтонианом $\tilde H$, но закон движения по траектории уже другой

[amon]

pogulyat_vyshel,
А есть какие-нибудь способы установить не считая гамильтониан, обладает ли данное преобразование таким мерзким свойством или нет? Поясню. Считался функциональный интеграл, и показалось, что каноническим линейным преобразованием он приводится к чему-то считабельному, но там в экспоненте стоит Лагранжево действие, и попытка его сосчитать привела к вышеописанному казусу.