Во-первых, Вы излагаете свои рассуждения недостаточно аккуратно. Более аккуратно --- это, например, так.
"Покажем, что если
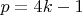
, то
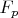
не содержит квадратного корня из

. Предположим противное, и
пусть

--- какой-либо корень. Поскольку

--- группа порядка

, то

. С другой стороны,

; противоречие. Значит, квадратного корня из

в
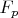
нет."
Заметьте, что это рассуждение к случаю
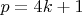
никак приспособить нельзя.
Во-вторых, Вы путаете аддитивную и мультипликативную структуру на

. Вообще, чтоб не было путаницы, лучше циклическую группу порядка

обозначать
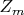
или

, кольцо вычетов по модулю

---

,
поле из

элементов
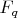
или

. И не путать, в случае чего, одно с другим. Хотя, часто, для экономии, символ

употребляют во всех трех смыслах, но по контексту и ситуации обычно понятно, рассматриваем мы его как группу, как кольцо, или как поле.
Если

--- группа, то корнем

-й степени из элемента

называют любой элемент

такой, что

. Он может быть не единственен. Когда я задавал вопрос про корень в
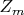
, я подразумевал именно группу, а не кольцо.
Короче, замените в том вопросе
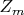
на

, и переосмыслите его опять.
Про квадратичные вычеты Вы помните правильно, только это не совсем по делу.
Её порядок равен

. Так как

простое, любой элемент кроме единичного

образующий. То есть порядок такого элемента также равен

Неверное утверждение. Возьмите хоть

.



