Исследовать при

на непрерывность функцию

Итак, подинтегральная функция непрерывна при

и

. Осталось доказать равномерную сходимость. Если разбить интеграл на два:

то для второго можно посчитать производную по

, которая будет равна

Производная равна нулю при

и это будет максимум. Тогда можно оценить

и

сходится при

. Таким образом, получим равномерную сходимость при

, но что делать с первым интегралом? Как доказать его равномерную сходимость, там же

стремиться к
 -- 22.05.2018, 02:14 --
-- 22.05.2018, 02:14 --Наверно нужно посмотреть на эквивалентную функцию при

. Тогда получим, что знаменатель функции
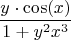
превращается в

, а числитель становится

. Интегралы по

в на отрезке
![$[0;1]$ $[0;1]$](https://dxdy-03.korotkov.co.uk/f/2/1/a/21ad730ee7df0b97abd700cb0f8426e682.png)
сходятся для обоих слагаемых

следовательно опять получим равномерную сходимость. Верно?



