Скалярность функций Грина

[Red_Herring]

Dr.Plank в сообщении #1313336 писал(а):

Я думаю да, правда не понимаю, как это влияет на то, скаляр ли функция Грина или нет

Это не влияет, но выкладки д.б. правильными.

Под выражением "скаляр" понимается инвариантность относительно лоренцевых преобразований, так? Ну а теперь заметьте что выражение зависит от только от лоренцева расстояния

[Dr.Plank]

Получается, что при домножении $G^{(2)}$ и $G^{(1)}$ на $\theta(t-t')$ они удовлетворяют исходному уравнению ?

Можно попробовать записать $G^{(1)}$ в виде:

$G^{(1)}(x-x', t-t')= $ $2c\pi\theta(c^2(t-t')^2-X^2)\theta(t-t')=2c\pi\theta((x^i-x^{i}')(x_{i}-x_{i}'))\theta(t-t')$,

где $x^i=(ct, x, 0, 0)$, $x^{i}'=(ct', x', 0, 0)$, $x^i-x^{i}'=(c(t-t'), x-x', 0, 0)$, $(x^i-x^{i}')(x_{i}-x_{i}')=c^2(t-t')^2-(x-x')^2$, но у нас тогда остается $\theta(t-t')$, а $(t-t')$ уже не инвариантно относительно преобразований Лоренца, и не накладывает ли вид (равенство нулю компонент $y$ и $z$) четырёхвекторов $x^i$, $x^{i}'$ ограничения на общность доказываемого утверждения?

Также не совсем понятно, что делать с $G^{(2)}$, знаменатель инвариантен относительно преобразований Лоренца, а аргумент функции Хевисайда требует дальнейших преобразований...

[Red_Herring]

Dr.Plank в сообщении #1313351 писал(а):

функции Хевисайда требует дальнейших преобразований.

Если вставить везде фактор $\theta(t-t')$, то то разность в аргументе можно заменить на разность квадратов.

Что касается $\theta(t-t')$ то его не будет, если воспользоваться другим определением ф.Грина, а здесь он инвариантен относительно тех Л.п. которые не переставляют прошлое с будущим. Все.

[Dr.Plank]

Всё-таки хотелось бы узнать, верны ли мои рассуждения?

Dr.Plank в сообщении #1313351 писал(а):

Можно попробовать записать $G^{(1)}$ в виде:

$G^{(1)}(x-x', t-t')= $ $2c\pi\theta(c^2(t-t')^2-X^2)\theta(t-t')=2c\pi\theta((x^i-x^{i}')(x_{i}-x_{i}'))\theta(t-t')$,

где $x^i=(ct, x, 0, 0)$, $x^{i}'=(ct', x', 0, 0)$, $x^i-x^{i}'=(c(t-t'), x-x', 0, 0)$, $(x^i-x^{i}')(x_{i}-x_{i}')=c^2(t-t')^2-(x-x')^2$

И если мы отбрасываем $\theta(t-t')$ в случае $G^{(1)}$, делая функцию Грина ни запаздывающей, ни опережающей, то разве $G^{(2)}$ не должна быть только запаздывающей, так как мы наоборот пользуемся наличием $\theta(t-t')$?

Из свойств функции Хевисайда нашел:

$\theta(ax+b)=\theta(x+\frac{b}{a})\theta(a)$,

если $a>0$, но, если мы им воспользуемся, то тогда получим:

$\theta(c(t-t')-\sqrt{X^2+Y^2})\theta(t-t')=\theta(c(t-t')^2-(t-t')\sqrt{X^2+Y^2})$,

что не очень похоже на квадрат интервала, или Вы имеете ввиду другое свойство?

[Red_Herring]

Ваше последнее равенство неверно. И я писал

Red_Herring в сообщении #1313356 писал(а):

то разность в аргументе можно заменить на разность квадратов.

Думайте сами

[Dr.Plank]

Тогда решение целиком я написал ниже, можете проверить на ошибки?

$G^{(2)}(x-x', y-y', t-t')=\frac {2c\theta(c(t-t')-\sqrt{X^2+Y^2})}{\sqrt{c^2(t-t')^2-X^2-Y^2}}$.

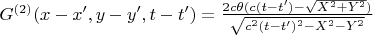
Знаменатель сам представляет скаляр, так как $x^i=(ct, x, y, 0)$, $x^{i}'=(ct', x', y', 0)$, $x^i-x^{i}'=(c(t-t'), x-x', y-y', 0)$, $(x^i-x^{i}')(x_{i}-x_{i}')=c^2(t-t')^2-(x-x')^2-(y-y')^2=A^2$,
где $A^i=(x^i-x^{i}')$,$\sqrt{c^2(t-t')^2-(x-x')^2-(y-y')^2}=|A|$

$c(t-t')-\sqrt{X^2+Y^2}>0$
$c^2(t-t')^2>X^2+Y^2$
$X^2+Y^2\geqslant0$ $ (1)$
$c(t-t')>0$ $ (2)$

Неравенство $ (1)$ справедливо само по себе, так как в нём стоит сумма квадратов действительных чисел, что по определению больше или равно нулю.
Неравенство $ (2)$ эквивалентно $\theta(t-t')$. Таким образом $\theta(c(t-t')-\sqrt{X^2+Y^2})$ можно заменить на $\theta(c^2(t-t')^2-X^2-Y^2)\theta(t-t')$, аргумент $\theta(c^2(t-t')^2-X^2-Y^2)$ можно выразить через четырёхвектор $\theta(c^2(t-t')^2-X^2-Y^2)=\theta((x^i-x^{i}')(x_{i}-x_{i}'))=\theta(A^2)$. В итоге получим:

$G^{(2)}(x-x', y-y', t-t')=\frac {2c\theta(A^2)\theta(t-t')}{|A|}$,

или для функции Грина не являющейся ни запаздывающей, ни опережающей:

$G^{(2)}(x-x', y-y', t-t')=\frac {2c\theta(A^2)}{|A|}$

Потом используем метод спуска:

$G^{(1)}(x-x', t-t')=2c\int\limits_{-\infty}^{\infty}\frac {\theta(c(t-t')-\sqrt{X^2+Y^2})}{\sqrt{c^2(t-t')^2-X^2-Y^2}}dY$
$c(t-t')-\sqrt{X^2+Y^2}>0$
c^2(t-t')^2>X^2+Y^2$
c^2(t-t')^2-X^2>Y^2$
\pm\sqrt{c^2(t-t')^2-X^2}>Y$
$c(t-t')>0$ - данное неравенство также требует добавления $\theta(t-t')$.

$G^{(1)}(x-x', t-t')=2c\int\limits_{-\sqrt{c^2(t-t')^2-X^2}}^{\sqrt{c^2(t-t')^2-X^2}}\frac {1}{\sqrt{c^2(t-t')^2-X^2-Y^2}}dY=\left. \arcsin(\frac{Y}{\sqrt{c^2(t-t')^2-X^2}}) \right|^{\sqrt{c^2(t-t')^2-X^2}}_{-\sqrt{c^2(t-t')^2-X^2}}=$ $ =2c( \arcsin(1)- \arcsin(-1))=2c\pi\theta(c^2(t-t')^2-X^2)\theta(t-t')$

Аргумент $\theta(c^2(t-t')^2-X^2)$ записываем в четырехмерном виде:

$c^2(t-t')^2-X^2=(x^i-x^{i}')(x_{i}-x_{i}')=B^2$

где $x^i=(ct, x, 0, 0)$, $x^{i}'=(ct', x', 0, 0)$, $x^i-x^{i}'=(c(t-t'), x-x', 0, 0)$, $(x^i-x^{i}')(x_{i}-x_{i}')=c^2(t-t')^2-(x-x')^2$, $B^i=(x^i-x^{i}')$

В итоге получим:

$G^{(1)}(x-x', t-t')=2c\pi\theta(B^2)\theta(t-t')$,

или для функции Грина не являющейся ни запаздывающей, ни опережающей:

$G^{(1)}(x-x', t-t')=2c\pi\theta(B^2)$

[Red_Herring]

Dr.Plank в сообщении #1313433 писал(а):

можете проверить на ошибки

Нет: слишком много букв в тривиальной задаче.

[Dr.Plank]

Ладно, спасибо за помощь, без Вас я бы долго с ней мучался!