Скалярность функций Грина

[Dr.Plank]

Доброго времени суток!
Очень нуждаюсь в вашей помощи!
Необходимо доказать или опровергнуть, что трёхмерная, двумерная и одномерная функция Грина являются скалярами и могут быть записаны в четырёхмерном виде. В качестве трёхмерной функции Грина я взял функцию Грина волнового уравнения:

$G^{(3)}(\vec{r}-\vec{r} ', t-t')=\frac {\delta(t-t'-\frac{|\vec{r}-\vec{r}'|}{c})}{|\vec{r}-\vec{r}'|}$,

после чего использовал метод спуска - проинтегрировал по координате $z$, чтобы получить двумерную функцию Грина:

$G^{(2)}(x-x', y-y', t-t')=\frac {2c\theta(c(t-t')-\sqrt{X^2+Y^2})}{\sqrt{c^2(t-t')^2-X^2-Y^2}}$,

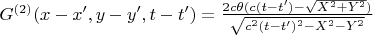
где $X=(x-x')$, $Y=(y-y')$ (при необходимости могу расписать более подробно), потом я опять использовал метод спуска, но только уже по отношению к координате $y$ и получил:

$G^{(1)}(x-x', t-t')=2c\pi\theta(c^2(t-t')^2-X^2)$.

Чтобы привести трёхмерную функцию Грина к скалярному виду, я воспользовался свойством $\delta$ функции:

$\delta(x^2-a^2)=\frac {1}{2a}\delta(x-a)+\frac {1}{2a}\delta(x+a)$,

вытекающим из

$\delta(f(x))=\frac {1}{|f'(x^*)|}\delta(x-x^*)$

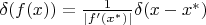
($x^*$ - корень $f(x)$), а также

$\delta(bx)=\frac {1}{b}\delta(x)$,

и получил в итоге:

$G^{(3)}(\vec{r}-\vec{r}', t-t')=\frac {c\delta(c(t-t')-|\vec{r}-\vec{r}'|)}{|\vec{r}-\vec{r}'|}=$ $(\frac {c\delta(c(t-t')-|\vec{r}-\vec{r}'|)}{|\vec{r}-\vec{r}'|}+\frac {c\delta(c(t-t')+|\vec{r}-\vec{r}'|)}{|\vec{r}-\vec{r}'|})\theta(t-t')=$ $2c \delta(c^2(t-t')^2-(\vec{r}-\vec{r}')^2)\theta(t-t')=2c \delta((x^i-x^{i}')(x_{i}-x_{i}'))\theta(t-t')$,

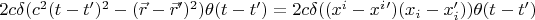
где $x^i=(ct, \vec{r})$, $x^{i}'=(ct', \vec{r}')$, $x^i-x^{i}'=(c(t-t'), \vec{r}-\vec{r}')$,

$(x^i-x^{i}')(x_{i}-x_{i}')=c^2(t-t')^2-(\vec{r}-\vec{r}')^2$.

Приведенное выражение для трёхмерной функции Грина говорит о том, что она является скаляром и её можно записать в четырёхмерном виде.
А вот с приведением двумерной и одномерной функции Грина у меня возникли трудности, а именно, проблемы с функцией Хевисайда: не знаю как её преобразовать подобным образом (если это вообще возможно), так как она не обладает свойствами, присущими дельта функции. Можно, конечно, выразить функцию Хевисайда через интеграл от дельта функции, но по-моему это никуда не ведёт, и должен быть другой метод, которого я, очевидно, не замечаю.
Буду очень благодарен за помощь!

[Red_Herring]

Напишите определение функции Хевисайда и тогда все поймете

[Dr.Plank]

Вы про то, что она кусочно-постоянная?

[Red_Herring]

Dr.Plank в сообщении #1313278 писал(а):

Вы про то, что она кусочно-постоянная?

Я просил написать определение.

[Dr.Plank]

Функция Хевисайда - кусочно-постоянная функция, равная нулю для отрицательных значений аргумента и единице — для положительных, или

$$ \theta(x)=\begin{cases} 0,&\text{если $x<0$;}\\ 1,&\text{если $x\geqslant 0$.} \end{cases} $$

[Red_Herring]

Хорошо, теперь посмотрите на аргумент; в $G^{(1)}$ уже все хорошо, но у вас ошибка (ф.Г. будет $0$ при $(t-t')<0$, т.ч. нужен еще множитель $\theta(t-t')$; а с $G^{(2)}$ аналогично.

[Dr.Plank]

С $G^{(2)}$ в принципе понятно, подкоренное выражение должно быть больше нуля, и, если $t-t'<0$, то тогда аргумент функции Хевисайда меньше нуля и она сама равняется нулю, но зачем домножать $G^{(1)}$ на $\theta(t-t')$, если там у нас $t-t'$ в квадрате, или я Вас не правильно понял?

[Red_Herring]

Dr.Plank в сообщении #1313293 писал(а):

зачем домножать

Можно использовать 2 определения функции Грина для эволюционной задачи. В данном случае у нас волновое уравнение.

1) $G_{tt}-c^2\Delta G=0$, $G|_{t=t'}=0$, $G_t|_{t=t'}=\delta (\mathbf{x}-\mathbf{x'})$. Тогда домножать не надо, но тогда только $G^{(1)}$ из ваших этому удовлетворяет.

2) Можно домножить на $\theta(t-t')$, тогда $G_{tt}-c^2\Delta G=\delta(t-t')\delta (\mathbf{x}-\mathbf{x'})$ и $G=0$ при $t-t'<0$, тогда только $G^{(2)}$ и $G^{(3)}$ из ваших этому удовлетворяют.

Ну и спуск "оставляет определение". Так что решите, какое из них вам хочется

[Dr.Plank]

Red_Herring в сообщении #1313299 писал(а):

2) Можно домножить на $\theta(t-t')$, тогда $G_{tt}-c^2\Delta G=\delta(t-t')\delta (\mathbf{x}-\mathbf{x'})$ и $G=0$ при $t-t'$, тогда только $G^{(2)}$ и $G^{(3)}$ из ваших этому удовлетворяют.

Ну и спуск "оставляет определение". Так что решите, какое из них вам хочется

Я изначально выводил функцию Грина для второго случая, но, к сожалению, не могу понять как связано домножение на $\theta(t-t')$ и то, что только $G^{(2)}$ и $G^{(3)}$ удовлетворяют данному уравнению...

-- 18.05.2018, 23:34 --

Может быть из-за того, что только две данные функции требуют домножения на функцию $\theta(t-t')$, которая, в свою очередь, обусловлена наличием $\delta(t-t')$ в исходном уравнении?

[Red_Herring]

Если вы использовали второе определение, то спуск от $G^{(2)}$ к $G^{(1)}$ неверный

[Dr.Plank]

Я использовал уравнение $\square{G}=\frac{-4\pi}{c}\delta(ct-ct')\delta(\vec{r}-\vec{r}')$

-- 19.05.2018, 00:08 --

Сам метод спуска:
$G^{(1)}(x-x', t-t')=2c\int\limits_{-\infty}^{\infty}\frac {\theta(c(t-t')-\sqrt{X^2+Y^2})}{\sqrt{c^2(t-t')^2-X^2-Y^2}}dY$
$c(t-t')-\sqrt{X^2+Y^2}>0$
c^2(t-t')^2>X^2+Y^2$
c^2(t-t')^2-X^2>Y^2$
\pm\sqrt{c^2(t-t')^2-X^2}>Y$
$G^{(1)}(x-x', t-t')=2c\int\limits_{-\sqrt{c^2(t-t')^2-X^2}}^{\sqrt{c^2(t-t')^2-X^2}}\frac {1}{\sqrt{c^2(t-t')^2-X^2-Y^2}}dY=\left. \arcsin(\frac{Y}{\sqrt{c^2(t-t')^2-X^2}}) \right|^{\sqrt{c^2(t-t')^2-X^2}}_{-\sqrt{c^2(t-t')^2-X^2}}=$ $ =2c( \arcsin(1)- \arcsin(-1))=2c\pi\theta(c^2(t-t')^2-X^2)$

[Red_Herring]

$c(t-t')-\sqrt{X^2+Y^2}>0 $ и $c^2(t-t')^2>X^2+Y^2$ не эквивалентны

[Dr.Plank]

Я так понимаю надо ещё наложить условие:
$X^2+Y^2\geqslant {0}$
и
$t-t'>0$

-- 19.05.2018, 01:01 --

Означает ли это, что нужно имеющееся выражение домножить на $\theta(t-t')$, чтобы было $2c \pi \theta(c^2(t-t')^2-X^2)\theta(t-t')$?

[Red_Herring]

Dr.Plank в сообщении #1313324 писал(а):

Означает ли это, что

А вы как думаете?

[Dr.Plank]

Я думаю да, правда не понимаю, как это влияет на то, скаляр ли функция Грина или нет