
(
А что это за гамма? Вы должны в пределе просто синус заменить на эквивалентную функцию -- и всё.
Тут ничего придумать не получается.
Это я посоветовал Вам применить к первому своему рассуждению, по-моему такой пример будет более строгим, нежели Ваши словесные рассуждения про значения

, при которых синус обращается в единицу. Просто подставьте эту последовательность в свой первый случай на интервале

Сойдет ли это за "понимание"?
А разве там в Зориче не доказывается, что показательная функция растет быстрее степенной, а логарифмическая -- медленнее.. Т.е. непонятно, о каком понимании речь, если там это обосновывается? Или Вы пытаетесь это заново вывести самостоятельно?
-- 18.05.2018, 16:58 --Чтобы показать, что такую замену можно использовать(могу ошибаться), нужно воспользоваться теоремой о пределе композиции функций и показать
Опять же, зачем что-то показывать, если можно просто воспользоваться теоремой о замене переменной? Примерно вот такая формулировка: если
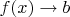
при

и

при

, то

при
 -- 18.05.2018, 17:17 --
-- 18.05.2018, 17:17 --Предлагаю Вам следующую (по-моему, довольно простую и понятную) схему доказательства того, что

(

,

):
1. Покажите, что при


2. Покажите, что

(с помощью неравенства о двух милиционерах)
3. Покажите, что

при

4. Покажите требуемое
Ну а потом заменой переменной покажете, что




