Вы не могли бы сюда эти уравнения выписать с какими-то минимальными коментами
Попытаюсь, но много букв получается. Эта деятельность Дирака связана с квантованием электродинамики. Число уравнений Максвелла в вакууме больше числа неизвестных и часть этих уравнений хочется объявить связями. Дирак предложил регулярную процедуру, которая для Максвелла не очень нужна, но про которую вспомнили Фаддеев с Поповым когда квантовали поля Янга-Милса. Дальнейшее - парафраз из Фаддеева, в части к квантовой механике отношения не имеющей.
Пусть дана механическая система с

степенями свободы и

связями,

- ее канонические переменные. Действие имеет вид
![$$
\int\left[\sum_{i=1}^n p_i\dot{q}_i-H(p,q)-\sum_a\lambda_a\varphi^a(p,q)\right]dt,\;a=1\dots m,m<n
$$ $$
\int\left[\sum_{i=1}^n p_i\dot{q}_i-H(p,q)-\sum_a\lambda_a\varphi^a(p,q)\right]dt,\;a=1\dots m,m<n
$$](https://dxdy-03.korotkov.co.uk/f/6/f/9/6f91e4dc3c5f47a1e4411e5e169773a682.png)
Дирак рассматривает вопрос о том, в каком случае такое действие определит обобщенную гамильтонову систему. В частности (Дирак и другие случаи рассматривает) это возможно, когда выполняется

(По Дираку это связь первого класса, бывают и другие) Скобки Пуассона (1,2) исчезают на поверхности связи. По Дираку эти скобки слабо равны нулю. Что бы сделать систему гамильтоновой надо добавить

дополнительных связей

для которых

Доказывается, что это возможно, можно в качестве переменных

выбрать

а соответствующие
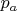
получатся решения

относительно

Тогда

и переменные

будут каноническими переменными обобщенной гамильтоновой системы.
Дирак рассматривает более общий случай, излагая это в свойственной ему манере говорить шарадами. Читать это не просто, но для любителей шарад интересно - вдруг какую еще никто не разгадал. Вон, Фейнман сообразил, что "corresponds to" по Дираковски означает "равно с точностью до множителя" и фейнмановские интегралы изобрел...