Если выборка не фиксирована и неизвестна выборочная дисперсия, ничего путного не получится, поскольку у Вас тогда задача из серии "ничего не дано, найти плотность".
Давайте я займусь телепатией и примерно напишу то, чего Вы хотите.
Задача: для данной реализации найти доверительную вероятность попадания генерального значения дисперсии в интервал
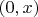
.
(По смыслу это именно то, чего Вы хотите.)
При известной выборочной дисперсии величина

имеет хи-квадрат распределение с

степенью свободы, а сама дисперсия, следовательно, обратное хи-квадрат распределение с тем же числом степеней свободы. Про него почитайте в англовики, например. Плотность там есть и можно вывести аналитически. Тем более, если степень свободы одна. Хуже с функцией распределения, там полезут неполные гамма-функции, если я навскидку не ошибаюсь.
https://en.wikipedia.org/wiki/Inverse-c ... stributionЭто если задача найти функцию распределения. Если задача - просто найти вероятности попадания в тот или иной интервал, то все проще и можно работать с величиной, обратной квадрату дисперсии, и смотреть, куда и с какими вероятностями попадает она. Ее распределение Вы знаете точно и сразу.
Сравните:
http://www.wolframalpha.com/input/?i=CD ... 5D,+0.2%5Dhttp://www.wolframalpha.com/input/?i=CD ... 1%5D,+5%5DЗвиняйте, мне на работу.
ps Но все равно задача как-то криво поставлена, не удовлетворена я этим.



