Пусть дана прямоугольная вещественнозначная матрица

(
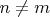
). Определим для нее обратную матрицу
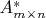
следующим образом:
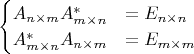
Здесь

— единичная матрица размера

. Можно ли элементарным образом показать, что матрицы
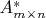
, удовлетворяющей обоим указанным соотношениям, не существует?
Пытался посмотреть на это с точки зрения системы линейных уравнений. Имеем

неизвестных (элементы матрицы
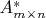
) и

уравнений.
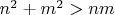
(для

), однако часть уравнений может быть линейно зависима (иначе для квадратных матриц обратных тоже не существовало бы). Навскидку определить максимальное количество линейно зависимых уравнений в данном случае вроде бы не получается. Поскольку
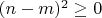
(причем равенство достигается только при
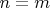
), то было бы неплохо, если бы это максимальное количество оказалось ограничено величиной

. В противном случае тут нужно искать совсем иной подход (если, конечно, некое элементарное доказательство в данном случае вообще возможно).



