Наверное предполагается, что случайные величины

,

,
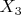
не просто являются нормальными, но являются компонентами нормального случайного вектора

. А раз так, то посмотрите в этом сборнике формулу для расчета произвольных моментов нормального вектора через производные характеристической функции. В вашем же решении есть ошибка -- вы предполагаете, что

,

,
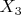
независимы в совокупности, но в условии про это ничего не сказано. Вместе с тем, матожидание это действительно равно нулю.
Просто возьмите формулу для харфункции нормального вектора, формулу для расчета произвольного момента, подставьте выражение для харфункции и получите ответ.