Приближение многочленами

[MChagall]

Две задачи на данную тему.
1) $K$ - компакт в $\mathbb{C}$. $\mathbb{C}\setminus K$ - не связно. $\hat{K}$ - это $K$ $+$ ограниченные компоненты дополнения.
$0\in \hat{K}\setminus K$. Нужно показать, что функцию $\frac{1}{z}$ нельзя на $K$ приблизить комплексными многочленами.

2) $D$ - внутренность единичного круга. $f$ голоморфна в $D$ и непрерывна на $\overline{D}$. Доказать, что существует такая последовательность многочленов $\left\lbrace P_n\right\rbrace$, что $P_n \to f$ на $\overline{D}$ равномерно при $n \to \infty$. Также доказать это для ограниченной области $G$, которая звездообразна относительно $a\in G$.
Аналитического продолжения перед этими задачами ещё не было.

По поводу 1. Есть путь, который я не могу довести до конца. Такой:
Из условия следует, что в нашем компакте существует замкнутая кривая $\gamma$, внутри которой находится $0$. Если $f$ равномерно приближается полиномами, то существует последовательность полиномов $\left\lbrace P_n\right\rbrace$, которая равномерно сходится к $f$ на $\gamma$. По критерию Коши $\forall \varepsilon >0 \exists N: \forall z\in \gamma \forall m,n\geqslant N \Rightarrow \left\lvert P_m(z) - P_n(z)\right\rvert<\varepsilon$. 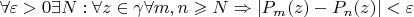По принципу максимума модуля эти неравенства верны $\forall z \in G$ ($G$ - область, ограниченная $\gamma$). Опять же, по критерию Коши последовательность $P_n$ равномерно сходится в $G$. 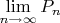По теореме Вейерштрасса $\lim\limits_{n \to \infty}^{}P_n$ - это функция, голоморфная в $G$. А на $G\cap K$ данный предел совпадает с $f$. И вот дальше я не знаю что делать. Хочется получить какое-то свойство $f$, которое не выполняется в точке $0$. Можно ли это решение довести как-то до конца? Или по-другому совсем надо?

2. В $D$ ведь работает теорема Рунге? Или нет? В круге я вообще могу в ряд Тейлора разложить. И мне надо показать, что этот ряд сходится на границе. Или не так всё?

[MChagall]

Для 1-й задачи, вроде, придумал вот что.
Из условия следует, что в нашем компакте существует замкнутая кривая $\gamma$, внутри которой находится $0$. Пусть на этой кривой наша функция равномерно приближается последовательностью полиномов $\left\lbrace P_n\right\rbrace$. Пусть $z_1=\min\limits_{z\in\gamma}z, z_2=\max\limits_{z\in\gamma}z$.
Рассмотрим кольцо $z_1<\left\lvert z\right\rvert<z_2$. В этом кольце $\frac{1}{z}$ раскладывается в ряд Лорана по степеням $z$. Пусть это последовательность $\left\lbrace Q_n\right\rbrace$.
Из единственности разложения следует, что на $\gamma$ $P_n=Q_n$. Но $z=0$ является неустранимой особой точкой функции $\frac{1}{z}$, значит содержит отрицательные степени $z$. Следовательно $P_n$ также должен их содержать. Значит, противоречие.
Верно ли такое рассуждение?

Для 2-й. В $D$ наша функция просто раскладывается в ряд Тейлора $P_n$, который и является искомой последовательностью. Надо доказать, что из непрерывности $f$ на границе следует сходимость на границе данного ряда. Верно? Только как это сделать?

[DeBill]

MChagall в сообщении #1304291 писал(а):

И вот дальше я не знаю что делать.

Как - что? Вы только что продолжили аналитически Вашу $f$ внутрь. Аналитическое продолжение - единственно (теорема единственности). А $f$ туда не продолжается (Не было ан.продолжения? Ну и ладно: сошлитесь на теоремы Мореры, делов то

MChagall в сообщении #1304291 писал(а):

Есть путь,

)
Гордитесь: то, что Вам пришло в голоау - один в один совпадает с "Шабат, п. 35"

MChagall в сообщении #1304423 писал(а):

В этом кольце $\frac{1}{z}$ раскладывается в ряд Лорана по степеням $z$

И я даже знаю как: $\frac{1}{z} = \frac{1}{z}$ (слева - функция, справа - ряд)
А кто такой $Q_n$, и почему он равен $P_n$?

-- 15.04.2018, 21:09 --

MChagall в сообщении #1304423 писал(а):

Верно? Только как это сделать?

А вот сделать это как то не шибко просто: будет мешать поведение на границе. Вот если бы была хотя бы гёльдеровость. то....
А без - можно попробовать так: рассмотреть функцию $f_t(z)= f(\frac{z}{t})$. При $t>1$, она хороша на единичном круге, и (теоерма Тейлора) частичные суммы ее ряда Тейлора сходятся на круге к ней равномерно. Но при $t \to 1+0$ функции $f_t$ тож сходятся равномерно (Доказать!)...

[MChagall]

DeBill в сообщении #1304473 писал(а):

Гордитесь: то, что Вам пришло в голоау - один в один совпадает с "Шабат, п. 35"

Так оттуда и взято! Так что гордиться нечем.

DeBill в сообщении #1304473 писал(а):

единственно (теорема единственности)

Не совсем понимаю механизм. У меня есть функции $f(z)=\frac{1}{z}$ и $g(z)=\lim\limits_{n\to\infty}^{}P_n$, которые совпадают на каком-то подмножестве $K$ области $G$. $g(z)$ голоморфна в $G$. Область $K$ условию теоремы о единственности удовлетворяет Почему $f(z)$ обязана существовать в $G$? Теорема о единственности в том же Шаббате (п. 22) говорит о функциях, голоморфных в области, а функция $\frac{1}{z}$ в точке $0$ не голоморфна.

DeBill в сообщении #1304473 писал(а):

А кто такой $Q_n$, и почему он равен $P_n$?

Ну $Q_n=\frac{1}{z}$. А равенство из единственности разложения. Верно ли такое решение?

-- 15.04.2018, 23:08 --

DeBill в сообщении #1304473 писал(а):

Гордитесь: то, что Вам пришло в голоау - один в один совпадает с "Шабат, п. 35"

Так оттуда и взято! Так что гордиться нечем.

DeBill в сообщении #1304473 писал(а):

единственно (теорема единственности)

Не совсем понимаю механизм. У меня есть функции $f(z)=\frac{1}{z}$ и $g(z)=\lim\limits_{n\to\infty}^{}P_n$, которые совпадают на каком-то подмножестве $K$ области $G$. $g(z)$ голоморфна в $G$. Область $K$ условию теоремы о единственности удовлетворяет Почему $f(z)$ обязана существовать в $G$? Теорема о единственности в том же Шаббате (п. 22) говорит о функциях, голоморфных в области, а функция $\frac{1}{z}$ в точке $0$ не голоморфна.

DeBill в сообщении #1304473 писал(а):

А кто такой $Q_n$, и почему он равен $P_n$?

Ну $Q_n=\frac{1}{z}$. А равенство из единственности разложения. Верно ли такое решение?

[DeBill]

MChagall в сообщении #1304533 писал(а):

механизм.

Пусть $g$ - тот самый предел. Рассмотрим функцию $h$, равную $f$ вне (и на) $\gamma$, и равную $g$ внутри $\gamma$. Эта функция будет везде аналитична (вообще то это не совсем очевидно, хотя Шабат тут об этом и говорит так, походя. Вместе с тем, в п. 40, лемма, в более простой ситуации, он дает подробное изложение этого места, на основе теоремы Мореры - существенно упрощаемое, если использовать "сильную" версию теоремы Коши, см. замечание там же) . По единственности, она должна совпадать с $f$ (там, где они обе определены). Но у $f$ в нуле - полюс, а $g$ в нуле голоморфна - противоречие.

[MChagall]

Видимо туплю, но так и не дошло вот что:

DeBill в сообщении #1304558 писал(а):

По единственности, она должна совпадать с $f$

Про какую единственность Вы говорите? Я знаю ту, что указана выше (Шаббат, п.35).

DeBill в сообщении #1304558 писал(а):

(там, где они обе определены)

Но у нас $f(z)$ просто не определена в точке $z=0$. Значит и совпадать не должны, вроде. Вот этот момент не понятен мне.

[vpb]

Существует ли кривая $\gamma$ ? Рассмотрим множество точек, которое в полярных координатах задается как
$K_1=\{(r,\varphi)\mid 0< \varphi\leq 2\pi,\ \ r=1+(1/2)\sin(1/\varphi)\}$,
и пусть $K$ --- его замыкание. Тогда, мне кажется, $K$ не содержит непрерывной замкнутой кривой, обходящей нуль.
(Может, я тут и ошибся, ввиду позднего часа).

DeBill, Вы на какое издание Шабата ссылаетесь? В том, что у меня, в соответствующих пунктах что-то совсем другое.

[MChagall]

MChagall в сообщении #1304586 писал(а):

Я знаю ту, что указана выше (Шаббат, п.35).

Имел ввиду Шаббат п.22 (теорема единственности)

vpb в сообщении #1304617 писал(а):

в соответствующих пунктах что-то совсем другое.

Чуть сдвинуто. У меня 1976 г, и там это п.36 (принцип максимума модуля), п.41 (принцип симметрии), п.22 (теоерма единственности).

[DeBill]

MChagall в сообщении #1304629 писал(а):

У меня 1976 г

А у меня -1969, однотомник.

MChagall в сообщении #1304586 писал(а):

Про какую единственность Вы говорите?

Про теорему единственности, п.21

-- 16.04.2018, 12:18 --

MChagall в сообщении #1304586 писал(а):

Но у нас $f(z)$ просто не определена в точке $z=0$. Значит и совпадать не должны, вроде.

Но вне нуля - должны, правда? И вот тут то и будет противоречие.

[MChagall]

DeBill в сообщении #1304649 писал(а):

будет противоречие

В том, что у $f(z)$ при стремлении к $z=0$ $f(z)$ стремится к бесконечности, а у полинома к конечному числу?

[Narn]

Я ТФКП учил лет 12 назад, так что извините, если чепуху напишу насчет первой задачи. Почему нельзя просто сказать: допустим, что есть равномерно сходящаяся последовательность многочленов. Тогда интегралы $\int_{\gamma} P_n(z) dz$ должны стремиться к $\int_{\gamma} \frac{1}{z} dz$, но от многочлена-то они всегда 0.

[DeBill]

Narn
И прекрасно все получится!

[vpb]

Спасибо за ссылки.

Позволю себе вновь привлечь внимание к примеру компакта $K$, указанному выше. Разве он ошибочен? Хотя, всякое конечно, возможно, может я чего-то очевидного не вижу...