Здравствуйте!
Недавно встретил в одной публикации некоторые соотношения. Я пока не буду приводить всю задачу целиком, там довольно много. Приведу лишь некоторую часть решения, которая несколько смущает. Имеются два условия следующего вида:

(1)

(2)
И выражение для
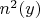
в виде следующего ряда:

(3)
Далее утверждается что, используя соотношения (1) и (2) совместно с (3), можно разложить

и

по степеням некоторого параметра

где
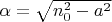
. Приведу выражение от авторов для

, оно менее громоздкое(думаю тут важно понять принцип):
![$y_2={\frac{\alpha}{\sqrt{c_1}}} \cdot [1 - \frac{c_2}{2 \cdot c_1^2} \cdot \alpha^2 + (\frac{7}{8} \cdot \frac{c_2^2}{c_1^4}-\frac{c_3}{2 \cdot c_1^3}) \cdot \alpha^4 + ...]$ $y_2={\frac{\alpha}{\sqrt{c_1}}} \cdot [1 - \frac{c_2}{2 \cdot c_1^2} \cdot \alpha^2 + (\frac{7}{8} \cdot \frac{c_2^2}{c_1^4}-\frac{c_3}{2 \cdot c_1^3}) \cdot \alpha^4 + ...]$](https://dxdy-04.korotkov.co.uk/f/b/5/9/b59930978d79e6986d07779a02f4591e82.png)
Вот здесь я не совсем понимаю как авторы получили подобное соотношение. Насколько я могу предположить здесь просто правые части выражений (2) и (3) приравниваются друг другу и, далее, мы считаем что у нас сложная функция

, которую можно разложить в ряд относительно параметра

а именно:

или:

Фантазируя дальше

предположу, что эту сложную функцию авторы просто раскладывают в ряд Маклорена. И вот здесь наступает ступор у меня. Наверное нужно применить формулу Фаа де Бруно и получить производные этой сложной функции чтобы построить ряд, но что-то не совсем понимаю как это лучше сделать. Или может быть я в своих предположениях ошибся и есть еще какие-то другие методы? Буду рад любой подсказке!



