AlexeyM88Обещанное в ЛС

1. "Занудство". Вы полагаете

, а потом считаете ответ до четвертого знака. Так нельзя, Вам же верить перестанут

Если Вы не указываете погрешность явно, то предполагается, что Вы указываете число в ответе до последней значащей цифры. А у Вас последние две значащие цифры ничего не значат.
2. "Фокус". Фокус называется "проверка на крайние значения".
Запишем ответ в виде формулы:

Как бы нам его проверить?
a) пусть это будет горизонтальная поверхность, и тянут горизонтально, а трение не нулевое. Тогда должно быть

. Подставляем в нашу формулу

. Ура! Совпало.
б) пусто это будет клин, трение ноль, а тянут параллельно поверхности клина. Тогда должно быть

. Подставляем в нашу формулу

и
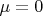
. Ура! Совпало.
Если нехватка времени, то на этом можно бы остановиться. Но если время есть, думаем дальше. И видим, что вот такая штука в знаменателе:

обнулялалсь в обоих случаях. Как бы нам проверить, хотя бы знак у неё? А очень просто.
Если тянут в направлении выше плоскости клина, то сила трения уменьшается; а если ниже, то увеличивается, и требуемая сила, чтобы сдвинуть груз будет больше. Проверяем, что если

, то сила

меньше, чем если

. Ура. Так и есть.
Ну и напоследок, можно задать вопрос, а при всех ли направлениях приложения силы груз можно сдвинуть? Видно, что не при всех, знаменатель может стать нулем. Запишем это:

, отсюда

. Вот при таком угле (и более крутых к поверхности) груз сдвинуть невозможно. Забавно, но это условие на угол между поверхностью клина и направлением силы, и никак не зависит от угла клина к горизонту.



