Пусть

гладкое многообразие. Рассмотрим векторное пространство над

(а можно и над

), порождённое связными

-мерными компактными ориентированными вложенными гладкими подмногообразиями

(в случае

-- ориентированными точками); причём если

и

-- подмногообразия, отличающиеся только ориентациею, то будем отождествлять

и

. Получающееся векторное пространство обозначим

и его элементы будем называть цепями. Определим гомоморфизмы

, задав их на порождающих элементах: пусть

--

-мерное подмногообразие

(ориентированное и т. д.), тогда

по определению есть (формальная) сумма связных компонент его границы (ориентация каждой компоненты индуцируется ориентацией

).
Получился цепной комплекс; группы гомологий этого комплекса будем обозначать
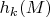
. Обычным образом определим циклы, границы и отношение гомологичности циклов.
Вопрос: в каком отношении полученные группы гомологий находятся к группам сингулярных гомологий

? Можно ли получить правильные гомологии, следуя каким-то похожим путём? Но только хочу именно через вложенные подмногообразия, а не просто какие-нибудь там гладкие отображения.
--------
Сначала что я знаю хорошего.
Во-первых, каждый наш цикл определяет некоторый сингулярный цикл, причём если 2 цикла гомологичны в смысле наших гомологий, то и в смысле сингулярных -- тоже. Значит, имеется гомоморфизм

.
Если я ничего не путаю, то этот гомоморфизм оказывается сюръективен, и это доказал Том (но, возможно, только в предположении, что

ориентируемо и компактно). Смотрите
Thom. Quelques propriétés globales des variétés différentiables, теорема II.29
(для любого целочисленного гомологического класса ориентируемого многообразия  существует целое ненулевое число
существует целое ненулевое число  , такое что класс
, такое что класс  может быть реализован подмногообразием)
может быть реализован подмногообразием). Насколько я понимаю, под "подмногообразием" там понимается именно гладко вложенное подмногообразие без края; кроме того, для ненулевых гомологических классов оно должно быть ориентируемым и компактным, потому что у неориентируемых или некомпактных многообразий старшая целочисленная группа гомологий нулевая.
Значит, наши гомологии могут быть только больше настоящих: единственная проблема может быть в том, что какие-то циклы на самом деле гомологичны, а у нас нет.
Так действительно бывает. Вот 3 возражения. Я их не сам придумал, а нашёл на
https://math.stackexchange.com/question ... ogy-groups: там у кого-то была очень похожая идея. А ещё там же рассмотрены некоторые случаи, когда всё работает правильно.
1)

имеет размерность континуум: проективные прямые в

реализуют попарно негомологичные классы.
2)

имеет размерность континуум: комплексные проективные прямые реализуют попарно негомологичные классы.
3) Можно доказать, что

не является границей никакого многообразия. Тем не менее оно вкладывается, например, в

. Следовательно,

.
Что касается первых двух возражений, то, насколько я понимаю, дело в следующем. Чтобы оказалось, что проективные прямые гомологичны, необходимо соотношение вида

; оно у нас может появиться, только если проективная прямая является связной компонентой границы какого-нибудь подмногообразия. Но у границы многообразия есть воротниковая окрестность, следовательно её можно сдвинуть так, чтобы она с собой не пересекалась, то есть её индекс самопересечения

. А у нас различные проективные прямые (что в вещественном, что в комплексном случае) пересекаются по одной точке (в которую проектируется прямая в

или
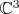
, являющаяся пересечением соответствующих плоскостей), следовательно самопересечение проективной прямой ненулевое, значит она не может быть связной компонентой границы никакого подмногообразия.
Что касается третьего возражения, то я его не понимаю. Чтобы

оказалось гомологично нулю, ему необязательно быть границей: можно быть связной компонентой границы. А оно умеет быть связной компонентой границы (например цилиндра над

). Может быть, есть вложенные подмногообразия

и

в

, диффеоморфные

, и подмногообразия

и

, такие что

, а

; тогда

, и всё хорошо.
А про первые 2 возражения: а давайте рассматривать в качестве образующих группы цепей не вложенные подмногообразия, а их изотопические классы? То есть считать дополнительно 2 диффеоморфных подмногообразия эквивалентными, если между их вложениями есть гладкая гомотопия по гладким вложениям. Тогда в этих 2 случаях всё нормально: проективную прямую в

можно передвинуть в себя же, но с противоположной ориентацией, и таким образом, наверно, получится правильный ответ

(ну если там кроме этих прямых ничего не ломается); а любые 2 проективные прямые в

можно совместить с сохранением ориентации, и получится правильный ответ

.
В каких-то ещё случаях получаются бесконечномерные гомологии?



