Интеграл

[thething]

mihiv
Вот в этой постановке меня что-то смущает, как-то слишком непрозрачно сформулировано.. Хотя, видимо, чтобы до этого додуматься, нам и была дана точка $z_0$.. Правда, это мы Вами решаем придуманную нами задачу

[mihiv]

thething
Мне кажется автор задачи всегда рассчитывает на определенную инициативу со стороны решающих (в разумных пределах) .

[DeBill]

А вот мне кажется, что задача поставлена вполне корректно: надо считать интеграл именно что по кривой (ну подумаешь - замкнутая она: для замкнутой кривой (рассматриваемой в "классическом смысле " - как класс эквивалентных путей), начальная и конечная точки - это разные точки, хотя, конечно , они и совпадают ). Так что регулярная ветвь логарифма на этой кривой имеется, и - все хорошо. Другое дело, что интегральную теорему нельзя применить непосредственно. Ну, ТС и проинтегрировал по частям, и стало хорошо - хочь он и напугался зачем то. А thething досчитал до ответа....

-- 20.03.2018, 23:59 --

И даже без интегрирования по частям, да: проведение разреза сразу превращает дурной интеграл в стандартный - от голоморфной внутре и непрерывной (почти) вплоть до границы

[thething]

Кстати, интегрирование по частям дает тот же ответ, а действий требуется меньше Надо только не забыть, что логарифм в одной и той же точке (в двойной постановке) будет принимать разные значения, отличающиеся друг от друга на $2\pi{i}$, а ко второму интегралу применить интегральную формулу Коши.

(Оффтоп)

Вот чего стоило в постановке задачи вместо слов "непрерывная ветвь" сразу написать "регулярная"?

[MChagall]

Решение, я так понял, найдено. Но я многого не понимаю. И начинать надо, видимо, издалека: разобраться с функцией $\operatorname{Ln} (z)$. Она, как я понял, многозначная из-за периодичности экспоненты ($\operatorname{Ln}(e^0)=0;\operatorname{Ln}(e^{2\pi i})=2\pi i$).
На $\mathbb{C}\setminus 0$ она не является непрерывной. Вопрос: а на каких множествах она будет непрерывной? Может кто-нибудь попытаться объяснить доходчиво?

[thething]

Логарифм -- многозначная функция из-за того, что в нем по определению стоит аргумент.

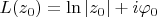
Если хотите способ попроще, то воспользуйтесь советом DeBill и доведите до конца способ способ с интегрированием по частям. У нас кривая не проходит через начало координат, следовательно, на ней логарифм не только непрерывен, но и даже регулярен (и область никакая не нужна. Доказывается просто проверкой условий Коши-Римана на кривой). При этом $L(z_0)=\ln\left\lvert{z_0}\right\rvert+i\varphi_0$ (в начале кривой), а $L(z_0)=\ln\left\lvert{z_0}\right\rvert+i\varphi_0+2\pi{i}$ (в конце кривой). Как видите, "физически" точка одна и та же, но аргумент прирос, вот и появилась многозначность.

Второй способ -- сделать разрез, как мы с mihiv описывали выше (по просьбе Markiyan Hirnyk я даже рассмотрел конкретный пример, а Вам остается его рассмотреть в общем виде. Суть не поменяется, только разрез не пойдет по действительной оси, а как-то в более общем направлении). Тогда уже получится область, в которой есть непрерывная и даже регулярная ветвь логарифма. Лично я предпочитаю второй способ просто потому, что в ТФКП он более распространен, чем приемы классического интегрирования из матанализа.

MChagall в сообщении #1298940 писал(а):

На $\mathbb{C}\setminus 0$ она не является непрерывной

На $\mathbb{C}\setminus 0$ она является многозначной, т.е. не совсем обычной функцией, с которой мы работать не привыкли. Чтобы с ней работать как обычно, надо выделять однозначные ветви, как правило, регулярные. Критерий выделения я приводил в сообщении выше.

thething в сообщении #1298593 писал(а):

Есть критерий выделения регулярной ветви $\operatorname{Ln}{z}$, согласно которому для выделения регулярной ветви необходимо и достаточно, чтобы область не содержала замкнутых кривых, обходящих начала координат.

[MChagall]

Правильно ли я тогда рассуждаю?
Берем любую ветвь логарифма. Пусть $\L(\gamma(0))=a$. Тогда при движении по $\gamma$ логарифм непрерывно доходит до значения $\L(\gamma(1))=a+2\pi i$. Этого и голоморфности $f(z)$ мне достаточно для существования и вычисления интеграла.
$\int\limits_{\gamma}^{}f'(z)L(z)dz=f(z_0) a+f(z_0) 2\pi i - f(z_0) a - \int\limits_{\gamma}^{}\frac{f(z)dz}{z}$. Для второго интеграла использую, что $f(0)=\frac{1}{2\pi i}\int\limits_{\gamma}^{}\frac{f(\zeta)d\zeta}{\zeta}$ для области, ограниченной $\gamma$.
В итоге $2\pi i f(z_0)-2\pi i f(0)$. Какие тонкости не учёл?

-- 22.03.2018, 12:30 --

Не учёл вот что. Я использую, что на $\gamma$ $L'(z)=\frac{1}{z}$. А для этого нужна не просто непрерывность, а голоморфность логарифма на $\gamma$. Но почему это так? (почему $L(z)$ голоморфна на$\gamma$?)

[thething]

MChagall в сообщении #1298994 писал(а):

Пусть $\L(\gamma(0))=a$

Нет, лучше так $L(z_0)=\ln\left\lvert{z_0}\right\rvert+i\varphi_0$, а после обхода $L(z_0)=\ln\left\lvert{z_0}\right\rvert+i\varphi_0+2\pi{i}$. Так будет строго в рамках определения.

MChagall в сообщении #1298994 писал(а):

Не учёл вот что. Я использую, что на $\gamma$ $L'(z)=\frac{1}{z}$. А для этого нужна не просто непрерывность, а голоморфность логарифма на $\gamma$. Но почему это так? (почему $L(z)$ голоморфна на$\gamma$?)

Голоморфность (регулярность) проверяется по условиям Коши-Римана.

Не забудьте при получении ответа учесть избранную ориентацию по кривой, т.е. Вы получите ответ либо с одним знаком, либо с другим. Так вот, необходимо указать, при какой ориентации получен именно Ваш ответ

[MChagall]

thething в сообщении #1299006 писал(а):

Голоморфность (регулярность) проверяется по условиям Коши-Римана

Для этого нужно как-то задать $L(z)$.
$L(\gamma(t))=L(r(t)e^{\varphi(t)})=\ln(r(t))+i \varphi(t)=\ln(r(t))+i \varphi_0+2\pi it$, где $r(0)=\ln\left\lvert z_0\right\rvert$. Но что-то при таком способе условия Коши-Римана не очень проверяются у меня. Может по-другому задать?

[thething]

$L(z)=\ln\left\lvert{z}\right\rvert+i\operatorname{\arg}{z}+2\pi{ki}$. Модуль и аргумент расписывать умеете?

[MChagall]

$u=\ln\sqrt{x^2+y^2}, v=\arctg\frac{y}{x}+2\pi k$
$u_x'=\frac{x}{\sqrt{x^2+y^2}}, v_x'=(\arctg\frac{y}{x})'=\frac{x}{\sqrt{x^2+y^2}}$.
Ну и вторую пару условий. Верно?

[thething]

Да, все верно

Но способ с разрезами, по-моему, более содержательный в рамках ТФКП. Можете и его попробовать, тем более что так считаются интегралы, которые нельзя взять по частям.

-- 22.03.2018, 14:45 --

Ой, недосмотрел, там же ж должно быть $v_y'$

[MChagall]

thething в сообщении #1299014 писал(а):

там же ж должно быть $v_y'$

Это я описался. Нашёл-то именно то.

[thething]

MChagall
Там производные без корней должны быть

[MChagall]

thething
Стыдно