Прямая сумма подпространств

[NEvOl]

Помогите разобраться пожалуйста. Есть утверждение, нужно понять верно оно или нет, и если не верно нужно как-то дополнить его, что бы оно стало верным.
Утверждение: Пусть $V$ - линейное пространство над полем $F$. Пусть $\forall i (1 \leqslant i \leqslant k ) {W}_{i} \leqslant V$ Причем $V = {W}_{1} + {W}_{2} + ... {W}_{k}$.
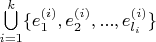
Пусть $\forall i (1 \leqslant i \leqslant k ) {e}_{i} = ({e}^{(i)}_{1}, {e}^{(i)}_{2}, ... , {e}^{(i)}_{{l}_{i}} )$ базис i-го подпространства. Тогда если базисом пространства $V$ является объединение базисов слагаемых подпространств ( т.е. если $\bigcup\limits_{i=1}^k \{ {e}^{(i)}_{1}, {e}^{(i)}_{2}, ... , {e}^{(i)}_{{l}_{i}} \}$ - базис пространства $V$) то сумма $V = {W}_{1} + {W}_{2} + ... {W}_{k}$ - прямая.

Я думаю что это не верно, потому что если рассмотреть множество геометрических векторов компланарных плоскости Оxz с базисом Ox, Oz и множество геометрических векторов компланарных плоскости Оyz с базисом Oy, Oz. Это подпространства векторного пространства $V_{3}$ - геометрических векторов в "пространстве". Их сумма даст $V_{3}$ и объединение базисных векторов даст базис $V_{3}$, но сумма не является прямой.
Я думаю что если добавить ограничение на то что базисы подпространств попарно не пересекаются, т.е. число векторов в базисе пространства V равно сумме $\sum\limits_{i=1}^{k} l_{i}$ тогда это будет верно, потому что мы получим что размерность суммы будет равна сумме размерностей.

Скажите пожалуйста, правильно ли я рассуждаю, может я что-то не так понимаю.

[vpb]

Правильно рассуждаете.

[DeBill]

NEvOl в сообщении #1298353 писал(а):

правильно ли я рассуждаю, может я что-то не так понимаю.

Да.Да: слова "объединение базисов" следовало понимать не так, как в Вашем "т.е."; для Вашего примера, объединение будет содержать ЧЕТЫРЕ вектора (Oz - дважды), и НЕ будет базисом. Так что исходное уиверждение - при правильном его понимании - верно.