Кельберт, Сухов, задачка.

[kirill94]

Задача 1.2.2. Лорд Вайл любит выпить виски, количество выпитого за день случайно, но известно, что он может выпить за день $n $ стаканов с вероятностью $\frac{1}{n!e}, n = 0, 1\ldots$ Вчера его жена леди Вайл, его сын Лидделл и его дворецкий решили убить лорда. Если он не пил виски в этот день, его должна была убить леди Вайл; если он выпил ровно один стакан, совершение убийства выпадало Лидделлу, в противном случае это должен был осуществить дворецкий. В два раза более вероятно, что леди Вайл прибегнет к отравлению, чем к удушению, дворецкий, напротив, выберет удушение с вероятностью в два раза большей, чем отравление, а Лидделл с равной вероятностью может выбрать любой из этих способов. Вопреки всем их усилиям, нет никакой гарантии, что лорд Вайл наверняка умрёт в результате какой-либо из попыток убить его, однако в случае удушения в три раза более вероятно, что он погибнет, чем в случае отравления.

Сегодня лорд Вайл мёртв. Какова вероятность того, что его убил дворецкий?


Застрял что-то на этой задачке, а конкретно: не получается подсчитать $\mathbb{P}[\text{Мёртв}|\text{убивал Дворецкий}]$. В книге это место не упомянуто, просто написано, что по сути равно
$\mathbb{P}[\text{Мёртв}|\text{отравлен}] \cdot \mathbb{P}[\text{отравлен}|\text{Дворецкий}] + \mathbb{P}[\text{Мёртв}|\text{задушен}] \cdot \mathbb{P}[\text{задушен}|\text{Дворецкий}]$.

Непонятно, почему это так. Ведь вообще говоря $\mathbb{P}[A|C] \not = \mathbb{P}[A|B] \cdot \mathbb{P}[B|C]$ в общем случае. Или я уже вообще туплю...

[warlock66613]

Это формула полной вероятности.

[kirill94]

warlock66613, всё равно не понимаю, если честно.
Обозначим $A = \{\text{Лорд мёртв}\}$, $C = \{\text{убивал Дворецкий}\}$. За $B_1, B_2$ обозначим $\{\text{использовали яд}\}, \{\text{использовали удушение}\}$ соответственно.
Вопрос: почему $\mathbb{P}[A|C] = \mathbb{P}[A|B_1] \mathbb{P}[B_1|C] + \mathbb{P}[A|B_2] \mathbb{P}[B_2|C]?$
Первое по определению равно $\frac{\mathbb{P}[AC]}{\mathbb{P}[C]}$.
Второе: $\sum\frac{\mathbb{P}[AB_i]}{\mathbb{P}[B_i]} \frac{\mathbb{P}[B_iC]}{\mathbb{P}[C]}$

[warlock66613]

kirill94, а формула

$$P(AC) = P(AC | H_1 C) P(H_1 C) + P(AC | H_1 \bar C) P(H_1 \bar C) + P(AC | H_2 C) P(H_2 C) + P(AC | H_2 \bar C) P(H_2 \bar C)$$

понятна?

[kirill94]

Да, мы разбили всё пространство на 4 события и применили формулу полной вероятности к событию AC. В таком случае я получаю

$$\frac{\matnbb{P}[AC]}{\matnbb{P}[C]} = \sum \frac{\mathbb{P}[ACH_i]}{\mathbb{P}[CH_i]} \cdot \frac{\mathbb{P}[CH_i]}{\mathbb{P}[C]}$$

А мне хочется доказать, что

$$\frac{\matnbb{P}[AC]}{\matnbb{P}[C]} = \sum \frac{\mathbb{P}[AH_i]}{\mathbb{P}[H_i]} \cdot \frac{\mathbb{P}[CH_i]}{\mathbb{P}[C]}$$

(Оффтоп)

:facepalm: такое ощущение, что я над чем-то простым сильно туплю

-- 19.03.2018, 17:53 --

Я к тому же ещё и со следующей задачей затупил из того же задачника

На станции стоят 3 телефонных автомата. Один из них не работает совсем, другой работает с вероятностью $\frac{1}{2}$, третий всегда работает. У нас есть три монеты. Мы кидаем монету в первый - он не работает. Затем мы дважды кидаем монету во второй, и оба раза получается сделать звонок. Какова вероятность, что второй аппарат полностью исправен?

Я сначала подсчитал вероятность $\mathbb{P}[\text{1 не работает} | \text{не сработал 1 раз}] = \frac{2}{3}$.
Следовательно, вероятность, что первый полуработающий - $\frac{1}{3}$.

Затем рассчитал вероятность $\mathbb{P}[\text{2ой работает} | \text{сработал 2 раза и 1ый не работает}] = \frac{4}{5}$
и $\mathbb{P}[\text{2ой полурабочий} | \text{сработал 2 раза и 1ый не работает}] = \frac{1}{5}$. Также нашёл вероятность
$\mathbb{P}[\text{2ой работает} | \text{сработал 2 раза и 1ый полурабочий}] = 1.$
В итоге у меня получилась вероятность того, что второй рабочий: $\frac{2}{3} \cdot \frac{4}{5} + \frac{1}{3} \cdot 1 = \frac{13}{15},$ и это неверный ответ.

[warlock66613]

kirill94 в сообщении #1298357 писал(а):

А мне хочется доказать, что

И это элементарно получается из предыдущего при условии независисости $H_i$ и $C$ (что имеет место в нашем случае).

[kirill94]

warlock66613
для этого надо показать, что $\mathbb{P}[H_1C] = \mathbb{P}[H_1] \mathbb{P}[C]$.
$\mathbb{P}[C] = 1 - \frac{1}{2e}$ из условия.

$$\mathbb{P}[H_1] = \mathbb{P}[H_1|\text{Жена}] \mathbb{P}[\text{Жена}] + \mathbb{P}[H_1|\text{Лиделл}] \mathbb{P}[\text{Лиделл}]+ \mathbb{P}[H_1|\text{Дворецкий}] \mathbb{P}[\text{Дворецкий}] = $$ $$ = \frac{1}{e} \cdot \frac{2}{3} + \frac{1}{e} \cdot \frac{1}{2} + (1 - \frac{2}{e}) \cdot \frac{1}{3} = \frac{1}{3} + \frac{1}{2e}$$

Также найдем

$$\mathbb{P}[H_1C] = \mathbb{P}[H_1 | C] \mathbb{P}[C] = \frac{1}{3} \cdot (1 - \frac{2}{e}) \not = $$ $$\not = \mathbb{P}[C] \cdot \mathbb{P}[H_1]$$

[warlock66613]

kirill94, согласен. Во всяком случае, из условия задачи ясно, что $P(A|H_i C) = P(A | H_i)$, а как это выразить через независимость и чего именно - надо подумать.

-- 19.03.2018, 21:47 --

$A$ и $C$ условно независимы (при условии $H_i$). Как это выразить более элегантно и/или без понятия условной независимости, не знаю.

-- 19.03.2018, 22:11 --

А вообще-то, в этой задаче совершенно не требуется считать $\mathbb{P}[\text{Мёртв}|\text{убивал Дворецкий}]$.

[kirill94]

warlock66613 в сообщении #1298407 писал(а):

kirill94
А вообще-то, в этой задаче совершенно не требуется считать $\mathbb{P}[\text{Мёртв}|\text{убивал Дворецкий}]$.

Почему? Если что - это просто одна из многих вероятностей, которые получились, когда принялся считать $\mathbb{P}[\text{убийца - Дворецкий | мёртв}].$ Да и самом задачнике, как я понял, предлагается её сосчитать в процессе решения...

А по поводу второй задачи, которую я тоже упоминал - не могли бы прокомментировать, что в ней может быть неправильно?

[warlock66613]

kirill94 в сообщении #1298424 писал(а):

Если что - это просто одна из многих вероятностей, которые получились

А, ну да. Я просто со всеми этими условными вероятностями уже забыл вопрос задачи.

-- 19.03.2018, 23:53 --

kirill94 в сообщении #1298424 писал(а):

А по поводу второй задачи, которую я тоже упоминал - не могли бы прокомментировать, что в ней может быть неправильно?

Не знаю, сложно анализировать ваше решение. Наверно, если распишите аккуратно, то можно будет сказать. Но ответ действительно неправильный: я решал без выкрутасов, "в лоб" и получил $6/7$.

[--mS--]

kirill94 в сообщении #1298424 писал(а):

А по поводу второй задачи, которую я тоже упоминал - не могли бы прокомментировать, что в ней может быть неправильно?

Как минимум, то, что Вы ищете какую-то безусловную вероятность, когда спрашивается про условную. А кроме того, используете какие-то непонятные связи вероятностей. Введите буквенные обозначения для событий и взгляните на последнее равенство:

$$ \mathsf P(A)=\mathsf P(B\mid C)\mathsf P(A\mid D\cap B)+ \mathsf P(E)\mathsf P(A\mid D\cap E) $$

- что это??

Заведите полную группу событий:

$H_1$ - 1-й не работает, 2-й полуработает, третий работает

$H_2$ - 1-й не работает, 2-й работает, третий полуработает

$H_3$ - 1-й полуработает, 2-й работает, третий не работает

$H_4$ - всё остальное.

Событие $A$ - первый автомат не сработал, второй сработал дважды.

$$\mathsf P(H_1)=\mathsf P(H_2)=\mathsf P(H_3)=\frac16, \quad \mathsf P(H_4)=\frac12$$

$$\mathsf P(A\mid H_1)=\frac14, \quad \mathsf P(A\mid H_2)=1, \quad \mathsf P(A\mid H_3)=\frac12, \quad \mathsf P(A\mid H_4)=0.$$

И ищите $\mathsf P(H_2\cup H_3 \mid A)=\mathsf P(H_2\mid A)+\mathsf P(H_3 \mid A)$ по формуле Байеса. Ответ дал warlock66613.

[kirill94]

--mS--
Действительно, всё получается.
Получаем $\mathbb{P}[A] = \frac{7}{24}$ по формуле полной вероятности, а затем просто формула Байеса.

В своем решении я рассуждал так:
Пусть мы кинули одну монетку и увидели, что автомат не сработал. Тогда у нас два варианта: он не рабочий (вероятность $\frac{2}{3}$) и он полурабочий (вероятность $\frac{1}{3}$).

Теперь отдельно рассмотрим оба случая:
1. Зная, что первый автомат нерабочий - какова вероятность, что второй окажется рабочим? У меня получилось $\frac{4}{5}$.
2. Зная, что первый автомат полурабочий - какова вероятность, что второй окажется рабочим? Вероятность 1.

И отсюда получалось $\frac{4}{5} \cdot \frac{2}{3} + \frac{1}{3} \cdot 1$.

-- 20.03.2018, 13:32 --

warlock66613
--mS--
Спасибо за помощь. Всё-таки часто не хватает интуитивного понимания вероятности, когда можно не расписывать вероятностное пространство дотошно и сразу что-то прикинуть-посчитать, а когда это необходимо, иначе легко запутаться.

[--mS--]

kirill94 в сообщении #1298495 писал(а):

Теперь отдельно рассмотрим оба случая:
1. Зная, что первый автомат нерабочий - какова вероятность, что второй окажется рабочим? У меня получилось $\frac{4}{5}$.
2. Зная, что первый автомат полурабочий - какова вероятность, что второй окажется рабочим? Вероятность 1.

И отсюда получалось $\frac{4}{5} \cdot \frac{2}{3} + \frac{1}{3} \cdot 1$.

Опять жонглирование словами, которые то и дело меняются. Обозначьте свои события буквами и попробуйте проверить финальную формулу.

При условии, что первый автомат нерабочий, вероятность, что второй окажется рабочим, равна $\frac12$. И это не то, что Вы находили. А итоговая формула вообще непонятно что вычисляет.

[kirill94]

--mS--
Я просто не понимаю, почему тут не проходит аналогий с урнами.
Первым я вытягиваю нерабочий автомат (вероятность $\frac{2}{3}$) или полурабочий (вероятность $\frac{1}{3}$) - эти вероятности найдены с помощью формулы полной вероятности с учетом, что одна монетка "не сработала". Но с этим вроде никто и не спорите.

Теперь я выкидываю этот автомат и работаю с двумя оставшимися.
По аналогии как в урновой схеме, если мы вытянули черный шар - рассматриваем одно вероятностное пространство, если белый - то другое.

В новом вероятностном пространстве, которое состоит у меня теперь из двух автоматов я ставлю задачу - я кидаю две монеты во второй автомат, и он оба раза срабатывает. Какова вероятность, что он рабочий?

Если первый вытянутый автомат был нерабочий, то у меня остается два варианта: (рабочий, полурабочий) для 2 и 3 соответственно и наоборот.
Обозначу:

$$A_1 = \text{Второй автомат рабочий}, \mathbb{P}[A_1] = \frac{1}{2}$$

$$A_2 = \text{Второй автомат полурабочий}, \mathbb{P}[A_2] = \frac{1}{2}$$

$$C = \text{Две монетки сработали}$$

$$\mathbb{P}[A_1 | C] = $$ $$ = \frac{\mathbb{P}[C|A_1] \cdot \mathbb{P}[A_1]} {\mathbb{P}[C|A_1] \cdot \mathbb{P}[A_1] + \mathbb{P}[C|A_2] \cdot \mathbb{P}[A_2]}$$

Также мы можем вычислить:

$$\mathbb{P}[C|A_1] = 1$$

$$\mathbb{P}[C|A_2] = \frac{1}{4}$$

И таким образом у меня и получается $\mathbb{P}[A_1 | C] = \frac{4}{5}$ в новом вероятностном пространстве.
Аналогично для второго вероятностного пространства я получаю вероятность 1.

[--mS--]

Видимо, причина в том, что Вы оперируете "условными событиями", которых не бывает. Давайте, я заведу ещё три события
$H_1$ - "первый автомат нерабочий", $H_2$ - "первый автомат полурабочий", $D$ - "первый звонок не удался".

Вы находите

$$ \mathsf P(A_1\mid CD) = \mathsf P(H_1\mid D) \mathsf P(A_1 \mid CH_1)+\mathsf P(H_2\mid D) \mathsf P(A_1 \mid CH_2). $$

Не вижу ни одной причины указанному равенству быть верным, даже если задействовать все имеющиеся взаимосвязи между событиями типа $A_1\subseteq C$, $H_1\subseteq D$ и т.п.

Давайте перейдём на язык вероятностного пространства. Я тупо перечислю все элементарные исходы и их вероятности. И покажу, долю чего среди чего требуется найти, и долю чего среди чего Вы находите.

Элементарный исход у меня будет иметь вид пяти символов: первые три - это перестановки букв Н, П, Р (автомат не работающий, полуработающий, работающий для 1, 2, 3 автоматов соответственно). Четвертый символ - результат первого звонка - 0 или 1, на пятом месте результат двух попыток со вторым автоматом - 00 или 01 или 10 или 11. Последний столбец - вероятности этих исходов.
Итак, всё пространство элементарных исходов:

$$\begin{pmatrix} \omega_1 & \text{Н} & \text{П} & \text{Р} & 0 & 00 & \frac16\cdot\frac14\\[2pt] \omega_2 & \text{Н} & \text{П} & \text{Р} & 0 & 01 & \frac16\cdot\frac14\\[2pt] \omega_3 & \text{Н} & \text{П} & \text{Р} & 0 & 10 & \frac16\cdot\frac14\\[2pt] \omega_4 & \text{Н} & \text{П} & \text{Р} & 0 & 11 & \frac16\cdot\frac14\\[2pt] \omega_5 & \text{Н} & \text{Р} & \text{П} & 0 & 11 & \frac16\\[2pt] \omega_6 & \text{П} & \text{Р} & \text{Н} & 0 & 11 & \frac16\cdot\frac12\\[2pt] \omega_7 & \text{П} & \text{Р} & \text{Н} & 1 & 11 & \frac16\cdot\frac12\\[2pt] \omega_8 & \text{П} & \text{Н} & \text{Р} & 0 & 00 & \frac16\cdot\frac12\\[2pt] \omega_9 & \text{П} & \text{Н} & \text{Р} & 1 & 00 & \frac16\cdot\frac12\\[2pt] \omega_{10} & \text{Р} & \text{Н} & \text{П} & 1 & 00 & \frac16\\[2pt] \omega_{11-14} & \text{Р} & \text{П} & \text{Н} & 1 & xx & \frac16 \end{pmatrix}$$

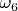
Требуется найти долю вероятности тех исходов, где на втором месте Р, среди всех исходов, оканчивающихся на $(0\ \ 11)$: это отношение вероятности исходов $\omega_5$, $\omega_6$ к вероятности $\omega_4$, $\omega_5$, $\omega_6$.

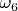
Что делаете Вы: сначала берём первые пять исходов отдельно (когда Н на первом месте). Их доля среди тех исходов, что кончаются на $(0\ \ xx)$, есть $2/3$. Далее ищете долю вероятности, которую составляет $\omega_5$ (вторая Р) среди $\omega_4,\omega_5$. Она оказывается $4/5$.

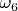
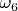
Потом берём исходы 6-й, 8-й (когда П на первом месте). Их доля среди тех исходов, что кончаются на $(0\ \ xx)$, есть $1/3$. Далее ищем долю вероятности $\omega_6$ среди $\omega_6$. Она оказывается $1$.

Итого получаете:

$$ \frac{\mathsf P(\omega_1,\omega_2,\omega_3,\omega_4,\omega_5)}{\mathsf P(\omega_1,\omega_2,\omega_3,\omega_4,\omega_5,\omega_6,\omega_8)}\cdot \frac{\mathsf P(\omega_5)}{\mathsf P(\omega_4,\omega_5)}+\frac{\mathsf P(\omega_6,\omega_8)}{\mathsf P(\omega_1,\omega_2,\omega_3,\omega_4,\omega_5,\omega_6,\omega_8)}\cdot \frac{\mathsf P(\omega_6)}{\mathsf P(\omega_6)}. $$

Тогда как нам нужна

$$ \frac{\mathsf P(\omega_5,\omega_6)}{\mathsf P(\omega_4,\omega_5,\omega_6)}. $$