Если кому-то будет интересен ответ,
на Mathematics Stack Exchange есть близкий вопрос. В ответе ссылки на полезные статьи. В кольце главных идеалов и в артиновом кольце определения эквиваленты. Так как

есть кольцо главных идеалов, оно не может быть примером. Ниже примеры колец, где определения не эквиваленты, из статьи.
Кольцо непрерывных функций на
![$[0, 3]$ $[0, 3]$](https://dxdy-04.korotkov.co.uk/f/f/1/8/f18842424afa022d9f70c2ba40e0ce9982.png)
. Пусть

есть функция, график которой есть ломаная, проходящая через точки

. Аналогично, график

есть

, график

есть

.

и

, то есть

и

ассоциированы по определению 0. Они не ассоциированы по определению 1.
Подкольцо произведения колец

и
![$\mathbb{Z}_5[X]$ $\mathbb{Z}_5[X]$](https://dxdy-02.korotkov.co.uk/f/1/4/4/144bf78de23fe11fd3d2c7ec8841b3eb82.png)
, подстилающее множество которого есть
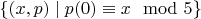
. Пусть

,

.

и

, то есть

и

ассоциированы по определению 0. Они не ассоциированы по определению 1.