Найдите набольшее значение

[epros]

eugensk в сообщении #1297429 писал(а):

Так в примере объект один, число 5, а x и у его два имени. Там же написано x=5, y=5. Я не понимаю, что здесь происходит.

Я тоже не понимаю. Вероятно, происходит ещё одна дурацкая постановка вопроса в стиле Sicker. Там было явно сказано про "два значения". Так что, наверное, речь всё же идёт о двух объектах, у которых просто случайно совпала некая характеристика.

[Mikhail_K]

epros в сообщении #1297444 писал(а):

Я тоже не понимаю.

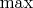
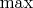
По-моему, постановка вопроса вполне корректна. Если $\max$ понимать функцией числового множества, то $\max(\{5,5\})=\max(\{5\})=5$. Ещё проще, если $\max$ понимать как функцию двух числовых переменных: тогда тоже $\max(5,5)=5$.

epros в сообщении #1297427 писал(а):

Это был намёк на то, что когда из множества двух ("как бы разных") объектов выбирается объект с максимальной некой характеристикой, то если эти характеристики одинаковы, выбраны должны быть оба объекта, а не какой-то один из них случайным образом. Например, выбирая в салоне автомобили с максимальным годом выпуска, мы должны выбрать все имеющиеся автомобили 2018 года, а не один из них.

То, что Вы пишете, называется ${\rm{Argmax}}$, а не $\max$.

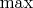
-- 14.03.2018, 21:26 --

По определению, ${\rm{Argmax}}_{x\in M}f(x)=\{y\in M\,|\,f(y)=\max\limits_{x\in M}f(x)\}$.
В Вашем примере, $M$ - множество автомобилей, $f(x)$ - год выпуска, $\max\limits_{x\in M}f(x)=2018$, а ${\rm{Argmax}}_{x\in M}f(x)$ - множество автомобилей с 2018 годом выпуска.

[epros]

Mikhail_K в сообщении #1297451 писал(а):

То, что Вы пишете, называется ${\rm{Argmax}}$, а не $\max$.

Да мне всё равно. Там речь-то была вообще о вопросе, который на разговорном языке прохожим задаётся. Поэтому читаем первую строчку, а все следующие за ней математические значки спокойно игнорируем. Если начать рассуждать, то, возможно, и получится достроить корректную постановку вопроса. Но суть-то не в этом, а в том, какие слова сказаны прохожему.

[Korvin]

miflin в сообщении #1297350 писал(а):

...формулу составляли либо обыватели, либо прохожые.

В развитие спонтанно образовавшейся подтемы в основном сабже.
Чтобы в имеющейся формуле множественной регрессии исключить функции мин макс (которые явно не от хорошей жизни), имхо следует результат вычисления по формуле регрессии подвергнуть нелинейному преобразованию типа функции Лапласа (с линейным преобразованием для смещения и изменения масштаба), что удержит искомое в реальных пределах, а затем еще раз по МНК уточнить коэффициенты при переменных (факторах). Уточненные коэффициенты вберут в себя изменения проистекающие от нелинейности функции Лапласа в центре, а хвосты функции Лапласа вберут в себя действие функций мин и макс.

[miflin]

(Оффтоп)

Вот долго сдерживался, но не выдержал...
Sicker, какие побудительные мотивы подвигли Вас на такую формулировку:

Sicker в сообщении #1297252 писал(а):

Вот такой вопрос можно задать обывателям и прохожим на улице

Для чего нужно задавать этот вопрос обывателям и прохожим?
Чтобы нарваться на встречный вопрос (от которого Вам может мало не показаться, храни Вас бог...), или где?