Здравствуйте.
Есть ряд

. Докажите, что для произвольного

последовательность имеет предел и найти его.
Я наткнулся на такое решение:
https://math.stackexchange.com/question ... os2n-1-tdtНо с определенного момента, я его не понял. Я напишу то, что я понял (больше для себя, чем для пользы дела), а вас попрошу объяснить, то что я не понял и то, что я понял неверно.
И так,

. Далее

- положителен при

и отрицателен при

Из-за симметри косинусов,

Выходит, что при

,
при

при

Так же, при


[/math].
Введем

Тогда

При


Введем

Тогда

Получается, что независимо от

ряд ограничен и монотонен, следовательно сходится.
Далее автор пишет, предположим, что

Тогда, если
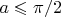
для достаточно больших


Это для меня неясно. Откуда взялся предел

? Что за

под интегралом?



