Доброго времени суток!
Заранее извините за неточные определения, так как я далеко не математик и даже близко не стою с ним.
Имеется кольцевая группа порожденная элементом равным 9 взятая по модулю.
При модуле 11 она выглядит так:

Так как





При небольших значениях модуля все легко решается в лоб. А вот когда модуль огромный, то хочется найти решение по-оптимальней. Собственно пока возникает 3 вопроса:
1. Есть ли какой алгоритм для нахождения индекса элемента?

Если брать пример выше, то, например, найти x при

, модуль равен 11. Ответ:
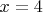
Гугл и википедия вторит, что "эффективные алгоритмы для решения задачи дискретного логарифмирования в общем случае неизвестны "
Ладно, если надо, то можем и поперебирать. Отсюда вытекает второй вопрос:
2. А можем ли мы определить, а есть ли вообще решения, чтобы за зря не заниматься перебором?
Опять, если брать тот же пример, то при m=7 решений нет.
Тут, наверное, тоже не все просто. Запустили перебор, нашли индекс. Все бы хорошо, но необходимо еще узнать порядок этой группы, то есть какое количество элементов в этой группе находится
3. Как определить порядок данной группы взависимости от модуля?
При

всего 5 элементов (9, 4, 3, 5, 1)
при

порядок 14 (9, 23, 4, 7, 5, 16, 28, 20, 6, 25, 22, 24, 13, 1)
А вот при

имеем (9, 40, 32, 1)
А если модуль будет несколько миллионов, то как высчитать?
Спасибо!



