уравнение Дирака

[Daniel_dgap]

Добрый день, господа. Назрел такой простой вопрос. Вот есть у меня некоторое уравнение Дирака (задача ставится в 2д), которое я привожу в систему:

$$ \Big( i\partial_x + (m+Bx)\Big) \varphi_1(x) = -k\varphi_2(x) $$

$$\Big( i\partial_x - (m+Bx)\Big) \varphi_2(x) = -k\varphi_1(x)$$

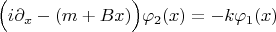
Из всего этого безобразия я перехожу к уравнению второго порядка для каждой из компонент. Например, для $\varphi_1(x)$:

$$(\partial_x^2 + (Bx + m)^2 + k^2 - iB)\varphi_1(x) = 0 $$

Для $\varphi_2$ уравнение будет таким же, только со знаком $+$ перед членом iB. Его решением являются функции Веббера. Ну, для некоторых нужд хватит рассмотреть и асимптотики, например. Но теперь, для получения функции $\varphi_2$, я подставляю решение $\varphi_1$ в уравнение системы, нахожу, таким образом,

$$\varphi_2(x) = -\frac{(i\partial_x + m + Bx)}{k} \varphi_1(x)$$

Но тогда второе уравнение начальной системы не удовлетворяется.
Как же тогда решить систему? и почему указанный способ не дает верного результата?

[amon]

У меня для Вас две новости, хорошая и плохая. Хорошая - что написанные уравнения линейны. а плохая - что к уравнению Дирака написанная система отношения не имеет. У Дирака четыре уравнения, а у Вас - два, и это не зависит от пространственных размерностей. Поэтому прежде чем что-то обсуждать хотелось бы понять то ли мы вообще обсуждаем.

[Daniel_dgap]

Ну меня же в 1+1 биспинор имеет две компоненты и матрицы Дирака являются первой и второй матрицами Паули. А в данном случае я ищу положительно частотные решения. Ну, на самом деле, положительно частотные или нет в этой конкретной ситуации значения не имеет.
Насчет линейности это да, неправильно написал. Извините)

[amon]

Я так понимаю, Вы какой-нибудь графен мучаете. Тогда уравнение будет $i\gamma^\mu\frac{\partial\psi}{\partial x^\mu}=m\psi.$ Вы уверены, что написали Ваш $Bx$ куда надо? Вроде как потенциал надо к $p_\mu$ добавлять, а не к $m.$

[Daniel_dgap]

Не, это не графен, а упрощенное КТП. И да, я вставил Bx исключительно правильно. Гриб с Мостепаненко писали случай, когда электрическое поле вида Et добавляется в длинную производную в уравнении Дирака. Правда у них решениями тоже являются функции Веббера. Но я рассматриваю в данном случае именно вышеописанную ситуацию и имею те уравнения, что привел выше.

[Red_Herring]

Перед $\partial_x^2$ должен быть "$-$". Роль $m$ неясна, т.к. ее можно убрать сдвигом по $x$.

[amon]

Daniel_dgap в сообщении #1295257 писал(а):

я рассматриваю в данном случае именно вышеописанную ситуацию

Ну, бог вам судья. Боюсь спрашивать, что Вы будете делать с релятивистской инвариантностью.

Касательно исходного вопроса. Может я чего пропустил, но если выполнено
$(\partial_x^2 + (Bx + m)^2 + k^2 - iB)\varphi_1(x) = 0 $
то, по-моему, второе уравнение выполняется тождественно:

$$ \begin{align} \varphi_2(x&) = -\frac{(i\partial_x + m + Bx)}{k} \varphi_1(x)\\ ( i\partial_x& - (m+Bx))(i\partial_x + m + Bx) \varphi_1(x) = k^2\varphi_1(x)\\ (\partial_x^2& + (Bx + m)^2 + k^2 - iB)\varphi_1(x) = 0. \end{align} $$

Red_Herring в сообщении #1295262 писал(а):

Перед $\partial_x^2$ должен быть "$-$".

Мне кажется, что с арифметикой все чисто (могу и ошибаться, время позднее). А c $m$'ом там и по физике какая-то беда, но если ТС настаивает...

[Red_Herring]

amon в сообщении #1295263 писал(а):

Мне кажется, что с арифметикой все чист

Действительно, там $+$ (поторопился)

[Daniel_dgap]

Отлично. Решение выглядит следующим образом:

$$ \varphi_1(x) = c_1 D_{-1-\frac{ik^2}{2B}}\Big( \frac{(1+i)(m+Bx)}{\sqrt{B}}\Big) + c_2 D_{\frac{ik^2}{2B}}\Big( -\frac{(1-i)(m+Bx)}{\sqrt{B}}\Big)$$

Для своих нужд я хочу найти асимптотическое решение системы. Опираясь на книжку Градштейна, при $t \rightarrow +\infty$ и пренебрегая массой, как фиксированным параметром, получаю:

$$ \varphi_1(x) = d_1 (\sqrt{2B}t)^{\frac{ik^2}{2B}} e^{\frac{iBt^2}{2}} $$

где $d_1$ некоторая константа, зависящая от импульса, не но от t. Хорошо. Теперь подставляем $\varphi_1$ в уравнение системы (в котором опять-таки пренебрегаем массой) и находим $\varphi_2(x)$:

$$ \varphi_2(x) = \frac{k}{2B} (\sqrt{2B})^{\frac{ik^2}{2B}} t^{\frac{ik^2}{2B} - 1} e^{\frac{iBt^2}{2}}$$

Легко видеть, что такой выбор функции $\varphi_2$ не удовлетворяет теперь уже второму уравнению системы. Так что вопрос как раз в этом. Как же тогда решать систему асимптотически?
Если не пренебрегать массой, все равно получается та же ерунда

[Daniel_dgap]

там везде, конечно, x, а не t

[v_n]

По моему, ваша функция $\varphi_2(x)$ с точностью до членов порядка $1/{x^2}$ удовлетворяет уравнению вашей системы. Мой совет - не пользоваться табличной асимптотикой функций, а получить все непосредственно. Представьте $\varphi(x)$ в виде $e^f$. Тогда нетрудно получить разложение для $f_x$ по степеням $1/x$. Учтите только , что возможно два типа разложения, как $f_x=iBx+a/x +...$ так и $f_x=-iBx+a/x +...$, которые дадут две разные асимптотики. Учитывая достаточное количество членов разложения вам легче будет понять с какой точностью выполняются равенства и как различные асимптотики для $\varphi_1$ и $\varphi_2$ переходят друг в друга при дифференцировании.

[Daniel_dgap]

v_n
Вы правы, с данной точностью решение $\varphi_2(x)$ действительно удовлетворяет системе, но, в конечном итоге хотелось бы еще написать нормировку на эти решения. Например, следующую из Вронскиана. Но в данном виде взятые $\varphi_1$ и $\varphi_2$ дают вронскиан, зависящий от времени, чего, конечно же, быть не должно

[Daniel_dgap]

нет, наврал. Все-же Вронскиан не зависит от времени, если смотреть в приближении до 2 порядка. Извините, не умею считать.
Наверное, раз уж у меня $\varphi_2(x)$ на порядок по x меньше, чем лидирующий член разложения $\varphi_1(x)$, то в асимптотическом разложении $\varphi_1(x)$ мне нужно держать и члены порядка $x^{\frac{ik^2}{2B} - 1}$

[amon]

Daniel_dgap в сообщении #1295431 писал(а):

в асимптотическом разложении $\varphi_1(x)$ мне нужно держать и члены порядка $x^{\frac{ik^2}{2B} - 1}$

Либо наоборот, считать $\varphi_2$ нулем и не мучаться.

[Daniel_dgap]

amon в сообщении #1295437 писал(а):

Daniel_dgap в сообщении #1295431 писал(а):

в асимптотическом разложении $\varphi_1(x)$ мне нужно держать и члены порядка $x^{\frac{ik^2}{2B} - 1}$

Либо наоборот, считать $\varphi_2$ нулем и не мучаться.

так, я полагаю, нельзя сделать, потому что при поиске отрицательно-частотных решений я получаю систему уравнений, эквивалентную вышенаписанной, с единственной разницей в том, что справа функции домножаются на k, а не на -k. Если выбросить $\varphi_2(x)$, то отрицательно-частотное решение будет совпадать с положительно-частотным. А это уже ерунда какая-то