Значит, нужно многочлен из

домножить, например, на многочлен

, чтобы при переходе в
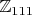
получить приведенный.
Многочлен с коэффициентами из

называется многочленом не
из 
, а
над 
. Если Вы имеете в виду, что надо взять многочлен

(над

) и потом рассмотреть его образ в
![${\mathbb Z}_{111}[X]$ ${\mathbb Z}_{111}[X]$](https://dxdy-03.korotkov.co.uk/f/a/8/b/a8b4d9e49e2bc97d63f732fcea455b3782.png)
, то это, конечно, будет многочлен со старшим коэффициентом

, но сомневаюсь, что тот, который нам нужен.
И еще. По моему, учебник Городенцева весьма хаотичен. Галопом по Европам, так сказать. Думаю, что даже продвинутым студентам НМУ в нем нелегко что-либо понять. Лучше читать Кострикина или Винберга.
-- 25.02.2018, 17:54 --Собственно, по задаче. Подсказка: придумайте-ка некий многочлен из
![${\mathbb Z}_{111}[X]$ ${\mathbb Z}_{111}[X]$](https://dxdy-03.korotkov.co.uk/f/a/8/b/a8b4d9e49e2bc97d63f732fcea455b3782.png)
степени 3, обращающийся в нуль при всех

.