Появилась ещё одна 'проблема', видимо имеющая элементарное решение но я в силу своего невежества его не знаю. Итак, нам известно преобразование Лапласа

существующее на всей правой полуплоскости и зависящее от набора параметров

. Необходимо узнать, является ли оригинал неотрицательной функцией или нет. Мои мысли следующие - мы можем определить новую функцию
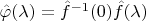
, теперь если её оригинал неотрицателен - это плотность вероятности. Но тогда

для

. Но мне это как критерий не нравится, во всяком случае на нужных нам функциях его применять очень неудобно. Есть ли что-нибудь получше? Спасибо.
P.S.Мужскую часть форума с праздником!



