Добрый день!
В равнобедренной трапеции диагонали пересекаются под углом 60 градусов. Найдите диагонали и нижнее основание трапеции, если верхнее основание 3 м, а боковая сторона трапеции 4 м.
Решение.
Необходимо решить задачу, не используя теорему синусов и более сложный инструментарий. Сама задача - из раздела "Теорема косинусов".

Трапеция равнобедренная, поэтому

,

.
Углы

равны 60 градусов,

градусов.
Отсюда в равнобедренных треугольниках
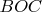
и
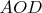
углы при основаниях

и

равны 30 градусов.
Найти диагональ

можно было бы по теореме косинусов, но для этого потребуется один из углов трапеции, которые неизвестны. Поскольку

- высота трапеции, угол

- прямой. Тогда угол

Но для нахождения градусной меры угла

необходим ещё угол

. Его нахождение позволило бы определить длину диагонали

. Зная, диагональ, по той же теореме косинусов легко определить нижнее основание

...



