Продолжаю прорешивать задачи из книжки Давидовича и ко
http://www.mccme.ru/free-books/57/davidovich.pdf.
В этой теме - листок 17.
Начиная с этого листка я решил изменить свой подход. Предыдущие листки я делал очень долго (по 2-3 месяца), и мое прохождение этого курса затянулось. Теперь я буду делать не все задачи подряд, а выборочно, только самые важные для понимания (по вашим рекомендациям). Я также буду меньше внимания уделять стилистике своих доказательств, чтобы не тратить на это время. Прошу от форумчан указывать мне только на серьезные ошибки и пробелы в доказательствах, и не сильно обращать внимание на второстепенные недочеты.
По итогам ЛС-общения с одним заслуженным участником этого форума по поводу этого листка я беру из него следующие задачи: 1.в, 1.г, 2, 4, 5, 8 и одну на выбор из 9* и 10*.
Определение 1.
Функция

называется равномерно непрерывной, если для любого

найдется

, для которого при любых

, таких что

, выполняется условие

.
Задача 1.
Являются ли следующие функции равномерно непрерывными:
в)

Неожиданно я застопорился уже на этой первой задаче.
Для начала выпишем отрицание определения равномерной непрерывности:


Подозреваю, что

не является равномерно непрерывной, но затрудняюсь это показать строго. Подозреваю, надо брать иксы с интервала
![$]0,1[$ $]0,1[$](https://dxdy-04.korotkov.co.uk/f/f/2/7/f27d1a8ebacee1389ff26e63ae97666182.png)
. Понятно, что надо использовать разность квадратов

. Уже убил кучу времени на эту задачу, буду благодарен если покажете мне как это правильно и кратко доказывать.
г)

Ответ: нет.
Пусть

и

-- произвольные числа. Возьмем

такие, что

и

. Тогда

.
Задача 2.
Верно ли, что равномерно непрерывная функция непрерывна?
Ответ.
Да. Из определения равномерной непрерывности следует определение непрерывности, т.к.

эквивалентно принадлежности

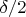
-окрестности некоторой точки, и аналогично

эквивалентно принадлежности


-окрестности некоторой точки.
Задача 4.
Доказать, что утверждение задачи 3 неверно для интервала (Задача 3. Непрерывная функция на отрезке равномерно непрерывна).
Доказательство.
Функция

непрерывна на
![$]a,b[$ $]a,b[$](https://dxdy-04.korotkov.co.uk/f/b/8/8/b88dc426f03d472a567196e74f3a404782.png)
и уходит на бесконечность при стремлении

к

слева.
Задавшись фиксированной разностью

и сдвигая оба икса на одинаковое расстояние все ближе к

слева, мы тем самым будем неограниченно увеличивать разность

. Т.е. разность значений

зависит не только от разницы соответствующих аргументов, но и от значений аргументов. Это противоречит определению равномерной непрерывности.
Задача 5.
Пусть

и

— равномерно непрерывные функции на

. Верно ли, что функции

и

равномерно непрерывны?
Ответ.

-- да.
По условию, для любого

существуют

такие, что для любых

из

следует

и

.
С применением неравенства треугольника,


т.е. определение равномерной непрерывности выполнено.

-- нет.
Контрпример: пусть

, тогда

-- не является равномерно непрерывной (задача 1.г).



