Да там

Да, теперь правильно.
Но в методе svv не понятно как все работает. Почему надо брать корень из определителя? Подход iifat показывает суть всего происходящего. Задачу проще решать методом svv, но хочется понять почему это так.
Давайте я расскажу немножко нестрашной теории, в надежде, что всё прояснится и станет на свои места.
Возьмём трёхмерное евклидово пространство
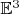
, хотя всё легко обобщается и на случай

. Пусть есть линейно независимая система векторов

и другая система векторов

. Между ними есть связь:

(по дважды повторяющимся индексам подразумевается суммирование), то есть
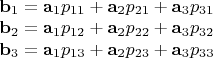
Коэффициенты

образуют
матрицу перехода от системы  к системе
к системе 
.
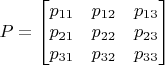
Обратите внимание, что элементы, стоявшие в формулах перехода в одной строке, в матрице выстроились в столбик; так принято.
Напомню, что объём параллелепипеда, построенного на векторах
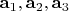
, мы обозначаем

. Справедливо утверждение (его обоснованием сейчас не будем заниматься):

Если

— матрица перехода от

к

, то

.
Матрица перехода связывает две системы векторов, а её определитель связывает два разных объёма.
Наоборот, матрица Грама составляется из попарных скалярных произведений векторов одной системы. Выясним, какое отношение она имеет к объёмам.
Обозначим матрицу Грама системы

через

с элементами

,
а матрицу Грама системы

через

с элементами

.
Следующий шаг Ваш. Попробуйте доказать, что


, то есть
