Почему интуиция? Я же проводил определенные рассуждения, которые и подтверждают "народную интуицию". )
Требование равновероятности повышает вероятность появления альтернативного исхода после подряд идущих событий. Естественно, при условии постоянства вероятностей исходов.
Печально... По-видимому, тут пора задать вопрос, как именно определяется вероятность какого-либо исхода (для конечного множества возможных исходов). Напишите определение.
Википедия утверждает, что вероя́тность — степень (относительная мера, количественная оценка) возможности наступления некоторого события.
Вы собираетесь бросать монетку, визуально оцениваете ее, видите тонкую ее толщину, аверс и реверс. Путем некоторых предположений формулируете гипотезу, что вероятность появления выпадения "орла" или "решки" будет
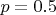
Подчеркиваю, сами броски еще не производились. Симметричность монеты и ее маленькая толщина являются некоторой гарантией равновероятности "орла" и "решки".
Когда компьютер генерирует "нолики" и "единички", вероятность их появления может быть произвольной.
До генерации что может говорить, что "единички" будут появляться с вероятностью

(например)?
Появление

и

- это случайное событие, вероятность которого нам неизвестна вначале.
Только сделав определенное количество испытаний по частоте появления 0 или 1 можем говорить о какой-то вероятности.
Так если установить доверительную вероятность

, то для подтверждения равновероятности ("нулевая" гипотеза) необходимо не меньше

бросков. Все комбинации, кроме
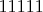
и

будут подтверждать "нулевую" гипотезу. Если все пять исходов одинаковы, значит следует увеличивать доверительный интервал.
Для доверительной вероятности

уже необходимо сделать не меньше

бросков, чтобы подтвердить "нулевую" гипотезу. Причем появление комбинаций

и

требует увеличения доверительного интервала для подтверждения "нулевой" гипотезы.
Для

необходимо сделать

бросков
Получается, что после ряда одинаковых исходов от последнего броска зависит принятие "нулевой" гипотезы с конкретной вероятностью или менять доверительный интервал в большую сторону. Неискушенные "бросатели" считают, что это монетка выпадает с какой-то вероятностью.



