
, так любое

делится нацело на

(тут тоже нужно доказательство, но оно мне известно).
Обозначим за

частное от деления

на

, то есть

.
По определению

. Следовательно:
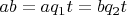
.
Получаем два равенства:
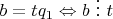
и

.
А значит

.
Пусть

не наибольший общий делитель, тогда существует

.
Но тогда

(по утверждению, доказанному в первом сообщении темы) и причем

. Получили противоречие.
Следовательно,

Все правильно?
grizzly, большое спасибо за наводку. Первую часть доказательства доказал именно по ней. А вот вторую часть сделал по своему. А как доказать так?
что она делится на на любой общий делитель этих чисел
-- 02.02.2018, 15:04 --Ну и вишенка на торте:
Теорема Доказательство
ДоказательствоОпустим скобки в записях общих делителей и кратных для простоты.
Выше было доказано, что

.
Опять же выше было доказано (в начале темы), что

для любых

.
Получается, что

.
Следовательно:

.
Но

, где

.
Итого имеем:

Сокращаем на

:

(Оффтоп)
Даже не подозревал о такой тесной взаимосвязи общих делителей и общих кратных друг с другом и с произведением

...



