Пусть есть два объекта, сигналы которых измеряет детектор. Проведено

опытов. Результат каждого опыта представляет собой пару чисел

и

, где

и

– измеренные значения,

и

– истинные значения,

,

и

– нормально распределенные случайные величины. Поскольку сигналы

и

в каждом опыте связаны коэффициентом

, есть предположение, что неопределенность измерения сигнала объекта можно уменьшить путём коррекции по сигналу другого объекта. Рассмотрим пример:
_______Объект 1___Объект 2
Опыт 1:___

________

Опыт 2:___

________
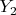
Опыт 3:___

________

Интуитивно хочется скорректировать сигнал

по формуле

.
Однако с математическим обоснованием возникли трудности. Прошу помочь советом.