an2ancan
Две пары точек на сфере определяют два больших круга на этой сфере. Выкиньте всё остальное и оставьте только две окружности от этих двух больших кругов. От взаимного расположения этих окружностей (угла между ними) ничего не меняется (вероятность что они совпадают нулевая). Итого у вас остается две окружности пересекающиеся в двух точках, и по две случайных точки на каждой окружности. Вот с этим "материалом" и "работайте".
Предстваим 2 окуружности на сфере, которые пересекаются в двух точках. (Скажем

и

). Попробуем прикинуть вероятность того, что дуга

, которая находится на одной из окружностей содержит, точку

. Это действительно так, если точки

и

лежат по разные стороны от

. Вероятность такого события равна

. Но при этом дуга
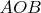
должна быть короче, чем
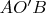
. В силу симметрии (оружность же), вероятность такого события тоже равна

. Получается вероятность, того что

содержит

равна:
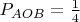
.
Симетрично, и для случая с

:
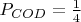
,
Т.е. вероятность того, что

и

пересекаются в точке

равна:
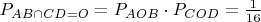
.
Но,

и

могут так же пересекаться и в точке

, при чем вероятность такого события равна

Тогда полная вероятность пересечения дуг равна сумме этих двух событий, т.е.

У меня есть вопрос:
Наверное, нужно еще и рассчитать вероятность того, что окружности пересекаются, ведь окружности могут быть паралеллями. Или как-то доказать, что вероятность такого события равна 0



