wrestИ Вам спасибо!
Как раз факторизации я и пугаюсь. Большие числа - большие проблемы.
Занимался извратом: представил 2924, как 36F+8, получил такое уравнение:

Представил значение в скобках как t, имею:

проанализировав, заметил, что решение есть, когда t задается формулой

, где n - целые положительные числа
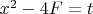
отсюда t+4F должно нацело извлекается из корня. Проделав некоторые преобразования получил еще одну формулу, которой задается t, при котором значения нацело извлекается из корня, для моего случая выглядит так:

Приравнивая две формулы, получаю еще одно Диофантово уравнение, которое еще все более усложнило )))
-- 24.01.2018, 13:33 --OttaБлагодарю!
Но это опять, как я понял, перебор значений. Я надеялся, что есть какая нибудь методика, сделав определенные преобразования, подставив коэффициенты имеющие и полученные получить результат, хотя бы на определенном (заданном) промежутке.
При малом значение F все легко найдется перебором, а если это число в какой нибудь большой степени, то перебор очень времязатратен
-- 24.01.2018, 13:39 --OttaБлагодарю!
Но это опять, как я понял, перебор значений. Я надеялся, что есть какая нибудь методика, сделав определенные преобразования, подставив коэффициенты имеющие и полученные получить результат, хотя бы на определенном (заданном) промежутке.
При малом значение F все легко найдется перебором, а если это число в какой нибудь большой степени, то перебор очень времязатратен



