Хоть с первого взгляда и кажется, что это классическая задача, на деле, есть подводные камни которые обойти не удалось.
Монгольский болотный грипп настолько редкий, что доктор ожидает встретить его раз в 10000. У больных всегда есть пятна (spots) и летаргия (lethargy). В 60% случаев больные мучаются жаждой (thirst) и в 20% сильно чихают (sneeze). При этом эти симптомы могут появляться и от других заболеваний: для пациентов у которых нету болотного гриппа вероятность появления пятен составляет 3%(spots), летаргии 10%(lethargy), жажды 2%(thirst) и 5%(sneeze) жалуются на постоянное чиханье. Эти четыре вероятности незаивисимы.
Показать что вероятность болеть гриппом составляет 80% если у пациента есть все 4 симптома. И 46% если есть все симптомы кроме чиханья.
Попытка решения:
Известно









Используя теорему Байеса


Вопрос заключается в том, как найти

, если мы знаем что они зависимы.
Есть только одна идея:
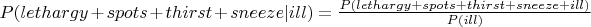

Мы знаем что,
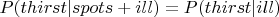

И тут идея загибается, потому что неясно как посчитать вероятность

Может ли кто-то обьяснить как бороться с этой задачей?
Спасибо
p.s. Добавляю оригинальный текст задачи:
Mongolian swamp fever is such a rare disease that a doctor only expects to meet once in every 10000 patients. It always produced spots and acute lethargy in a patient; in 60% of cases, they suffer from thirst and in 20% of cases from violent sneezes. These symptoms can arise from other causes: of patients that do not have this disease, 3% have spots, 10% are lethargic, 2% thirsty and 5% complain of sneezing. These four probabilities are independent.
Show that if you go to the doctor with all these symptoms, the probability of you having Mongolian swamp fever is 80% and that if you have all except sneezing the probability is 46%.



